


次: 名大前期文系
上: 解答
前: 東北大前期理系
-
- (1)
- 3点
 は半径1の円 C 上の点なので,
は半径1の円 C 上の点なので,
が成り立つ.
直線 z1w1 と直線 z3z2 が直交していることを示すためには,
が純虚数であることを示せばよい.ここで
 が実数なら原点と
が実数なら原点と  が1直線上に
あることになる.ゆえに実数ではなく,
が1直線上に
あることになる.ゆえに実数ではなく, は共役2虚数の差なので純虚数である.
ゆえに直線 z1w1 と直線 z3z2 は直交している.
同様に直線 z2w1 と直線 z1z3 も直交しているので
点 w1 は3点
は共役2虚数の差なので純虚数である.
ゆえに直線 z1w1 と直線 z3z2 は直交している.
同様に直線 z2w1 と直線 z1z3 も直交しているので
点 w1 は3点
 を頂点とする三角形の垂心になる
を頂点とする三角形の垂心になる
- (2)
-
 より w2 は C 上の点である.
より w2 は C 上の点である.
したがって確かに w2 は,2点  を通る直線上に点 z1 から下ろした
垂線またはその延長線が円 C と交わる点である.
を通る直線上に点 z1 から下ろした
垂線またはその延長線が円 C と交わる点である.
- (3)
- (1),(2)から
 は同一直線上にあり,その直線は
は同一直線上にあり,その直線は
 を通る直線と直交している.
したがって
を通る直線と直交している.
したがって  を通る直線に関して
を通る直線に関して が対称の位置にあることを示せばよい.
一般に原点と
が対称の位置にあることを示せばよい.
一般に原点と 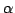 を結ぶ直線に関して z と対称な点は
を結ぶ直線に関して z と対称な点は
である.そこで
したがって, を通る直線に関してw1とw2 が対称の位置にある.
つまり 直線 z2z3上に点 z1 から下ろした垂線との交点は,
点 w1 と w2 を結ぶ線分の中点であることが示された.
を通る直線に関してw1とw2 が対称の位置にある.
つまり 直線 z2z3上に点 z1 から下ろした垂線との交点は,
点 w1 と w2 を結ぶ線分の中点であることが示された.
AozoraGakuen
2002-06-21

 が実数なら原点と
が実数なら原点と 


 が実数なら原点と
が実数なら原点と 
