

 次: 2. 東大前期理系
上: 2. 解答
前: 5.
次: 2. 東大前期理系
上: 2. 解答
前: 5.
 とおく.条件から
とおく.条件から
である.
したがって
 であるから
であるから
題意を満たす n が存在することは
 となる n が存在することと
同値である.
となる n が存在することと
同値である.
このような k が存在するような n が存在すれば
 となり,
となり,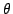 は有理数である.
逆に
は有理数である.
逆に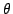 が有理数であるとし,
が有理数であるとし,
 とおく.
とおく.
 は
は
 である.
これを満たすk がとれる n としてn=qが存在する.実際k=p が条件を満たす.
よって題意が示された.
である.
これを満たすk がとれる n としてn=qが存在する.実際k=p が条件を満たす.
よって題意が示された.
AozoraGakuen
2002-03-01


 となり,
となり, とおく.
とおく.
 である.
これを満たすk がとれる n としてn=qが存在する.実際k=p が条件を満たす.
よって題意が示された.
である.
これを満たすk がとれる n としてn=qが存在する.実際k=p が条件を満たす.
よって題意が示された.