京大理(甲)4番
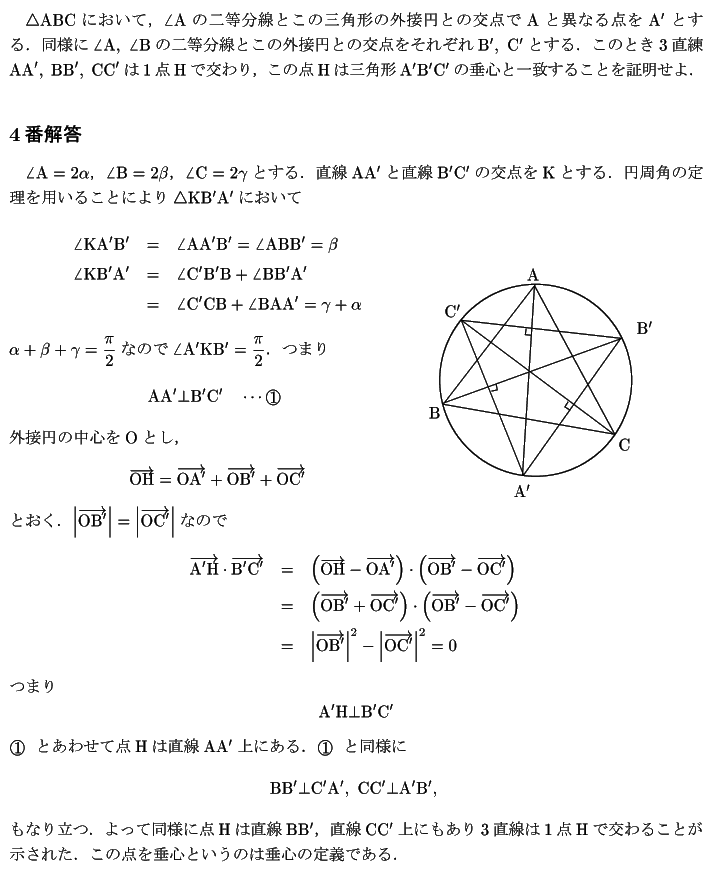
$ \bigtriangleup \mathrm{ABC} $ において,
$ \angle \mathrm{A} $ の二等分線とこの三角形の外接円との交点で $ \mathrm{A} $ と異な
る点を $ \mathrm{A}' $ とする.
同様に $ \angle \mathrm{B},\ \angle \mathrm{C} $ の二等分線とこの外接円との交点をそれぞ
れ $ \mathrm{B}',\ \mathrm{C}' $ とする.
このとき3直練 $ \mathrm{AA}',\ \mathrm{BB}',\ \mathrm{CC}' $ は1点 $ \mathrm{H} $ で交わり,
この点 $ \mathrm{H} $ は三角形 $ \mathrm{A'B'C'} $ の垂心と一致することを証明せよ.