信州大教育第2問
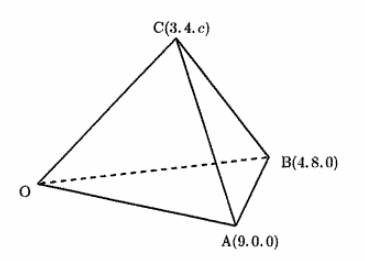
$ c $ を正の実数とする.空間において,原点 $ \mathrm{O} $ および3点 $ \mathrm{A}(9,0,0) $ , $ \mathrm{B}(4,8,0) $ , $ \mathrm{C}(3,4,c) $ を頂点とする四面体 $ \mathrm{OABC} $ がある。 辺 $ \mathrm{OA} $ の中点 $ \mathrm{L} $ を通り直線 $ \mathrm{BC} $ に直交する平面を $ \alpha $ , 辺 $ \mathrm{OC} $ の中点 $ \mathrm{M} $ を通り直線 $ \mathrm{AB} $ に直交する平面を $ \beta $ , 辺 $ \mathrm{AB} $ の中点 $ \mathrm{N} $ を通り直線 $ \mathrm{OC} $ に直交する平面を $ \gamma $ とする。 次の問いに答えなさい。
(1) 平面 $ \alpha $ , $ \beta $ , $ \gamma $ の交点を $ \mathrm{X} $ とする。点 $ \mathrm{X} $ の座標を求めなさい。
(2) 辺 $ \mathrm{OB} $ の中点を通り,直線 $ \mathrm{AC} $ に直交する平面上に点 $ \mathrm{X} $ はあるか。
理由を述べて答えなさい。
(3) 点 $ \mathrm{X} $ が四面体 $ \mathrm{OABC} $ の表面および内部にあるような $ c $ の値の範囲を求めなさい。