�P�D���
�@�ȒP�ɐ����ɂ��ĐU��Ԃ��Ă������D�@�P�����Ƃ́C
���ƁC0 �܂��͐��̎w�������������������킹�����̂ł���D
���̕������W���Ƃ����D
�@�������Ƃ͒P������a�ɂ���Č����������̂ł���D
�@�����Ƃ͒P�����Ƒ������̑��̂ł���D�������𐮎��̈Ӗ��ɗp���邱�Ƃ�����D
�@������ x �̏ꍇ
![]() �̂悤�ɋL���D
�̂悤�ɋL���D
�@�����ł��邩�ǂ����͌W���̖��ł͂Ȃ��D
![]() �������ł���D
�W���������ł�����̂𐮎��Ƃ����ƌ�����Ă���l�����邪����͂܂������D
�������ł���D
�W���������ł�����̂𐮎��Ƃ����ƌ�����Ă���l�����邪����͂܂������D
![]() ��
��
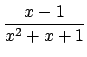 ���������łȂ��D���ꂼ��C�������C�L�����C�Ƃ����D
���������łȂ��D���ꂼ��C�������C�L�����C�Ƃ����D
���̖���������{�͎���2�̎����ł���D
(1)�@���@�̌����ƈ����藝�C��]�藝
�����͐����̏ꍇ�Ɠ��l�C������`����C�C�ӂ̐���
![]() �ɑ����̂��Ƃ����藧�D
�ɑ����̂��Ƃ����藧�D
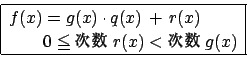
�@��������@�̌����Ƃ����C q(x),r(x) �����ꂼ�� f(x) �� g(x) �Ŋ��������C�]��Ƃ����D
�@���@�̌����͐����Ő��藧�D�����̏��@�̌�����p���Ď�����邳�܂��܂̐����� ��{�I�ɐ����ł����藧�D
�@���@�̓����ɂ����� g(x) ��
![]() �Ƃ���D g(x) �̎�����1�ł��邩��C
�]���0���C�܂�萔�ƂȂ�C���@�̎������̌`�ƂȂ�D
�Ƃ���D g(x) �̎�����1�ł��邩��C
�]���0���C�܂�萔�ƂȂ�C���@�̎������̌`�ƂȂ�D
��]�藝
�����藝
�����������ꂽ���q�������Ƃ����D���̂Ƃ����̂��Ƃ����藧�D
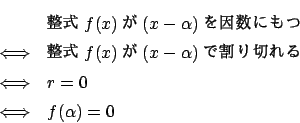
(2) �����̈�v�ƍP�����̒�`
![]() �� x �ɂ��Ă̐����ł���Ƃ�, ����3�̖���͓��l�ł���.
�܂�, ���̂Ƃ�, ���� A=B �� �P���� �ł���Ƃ���.
�� x �ɂ��Ă̐����ł���Ƃ�, ����3�̖���͓��l�ł���.
�܂�, ���̂Ƃ�, ���� A=B �� �P���� �ł���Ƃ���.
- 1.
�C�ӂ� x �̒l�ɑ���
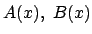 �͓���̒l���Ƃ�.
�͓���̒l���Ƃ�.
- 2. ���� A(x)=B(x) ���قȂ� n+1 �� x �̒l�ɑ��Đ��藧��.
- 3. A(x) �� B(x) �͓���̎��ł���. �܂�, �����������������������̍��̌W����������.
- 2. ���� A(x)=B(x) ���قȂ� n+1 �� x �̒l�ɑ��Đ��藧��.
�ؖ�
- 1.
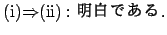
- 2.
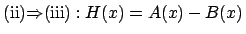 �� n ���ȉ��̐����ł���.
�� n ���ȉ��̐����ł���.
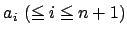 �̑��قȂ� ai �ɑ���, H(ai)=0 �ł��邩��, �����藝���,
�̑��قȂ� ai �ɑ���, H(ai)=0 �ł��邩��, �����藝���,
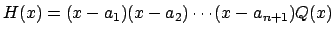 �ƈ������������. ����
�ƈ������������. ���� 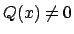 �Ȃ�,
���ӂ̎����� n �ȉ��ł���, �E�ӂ̎����� n+1 �ȏ�ƂȂ�. �����, �������N����.
����������, H(x)=0 . �܂�, A(x)=B(x) �ł���.
�Ȃ�,
���ӂ̎����� n �ȉ��ł���, �E�ӂ̎����� n+1 �ȏ�ƂȂ�. �����, �������N����.
����������, H(x)=0 . �܂�, A(x)=B(x) �ł���.
- 3.
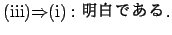
- 2.
�����, ����߂ďd�v�Ȓ藝�ł���. ���Ƃ���, f(x) ��������
���̂悤�ɖ��m�ɐ������Ȃ���Ȃ�Ȃ�.
2�D��
1�D�m81�N��嗝�n�n
��ӂ���
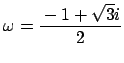 �Ƃ��@�� x ��
�Ƃ��@�� x ��
![]()
�@f(x) �� n �����Ƃ���
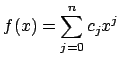 �Ƃ����ƁC
�A���͎��̂��Ƃ��Ӗ�����D
�Ƃ����ƁC
�A���͎��̂��Ƃ��Ӗ�����D
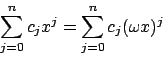
�@���������� f(x) ��3�̔{�����̍��ȊO�͌W����0�ƂȂ�C x3 �̑������ɂȂ邱�Ƃ��킩��D �܂��ӂ������ꂽ�D
2�D�m91���������n�n
- 1.
�� y=0 ��������ƁC
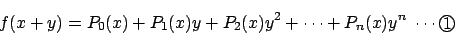 f(x)=P0(x)��������D�܂��C
f(x)=P0(x)��������D�܂��C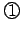 �� y �Ŕ��������
�ƂȂ�C���̎��� y=0 ���������
�� y �Ŕ��������
�ƂȂ�C���̎��� y=0 ���������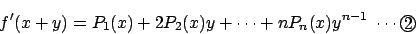 f'(x)=P1(x)��������D����� y �Ŕ���������ƂȂ�̂ŁC���l�ɂ���
f'(x)=P1(x)��������D����� y �Ŕ���������ƂȂ�̂ŁC���l�ɂ���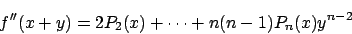 ��������D
��������D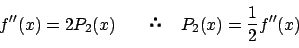
���ɁCf(x+y) �� x �� y �̎����̍��v����� n �ł���C����� Pn(x) �͒萔�ł���D
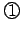 �� x=0 ���������
�ƂȂ�D�܂� f(x) �̍ō������̌W���� Pn(x) �ł��邱�Ƃ������Ă���D
�� x=0 ���������
�ƂȂ�D�܂� f(x) �̍ō������̌W���� Pn(x) �ł��邱�Ƃ������Ă���D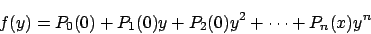
- 2. f(x) �̎�����
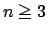 �Ɖ��肷��D
����C
�Ɖ��肷��D
����C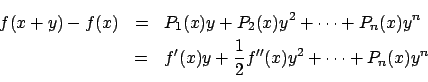
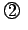 �� y �� cy �ɒu��������ƁC
�� y �� cy �ɒu��������ƁC
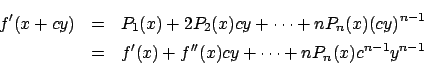
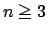 ���W�����r����ƁC
���W�����r����ƁC
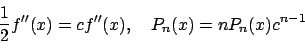
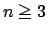 ���
���
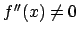 �ł��邩��C
�ł��邩��C
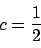
�܂��C
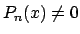 ���C
���킩��C���ꂩ�� 2n-1=n �����_�����D
���C
���킩��C���ꂩ�� 2n-1=n �����_�����D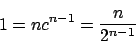
�Ƃ��낪
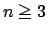 ���
�ƂȂ肱�̌��_�Ɩ�������D
���
�ƂȂ肱�̌��_�Ɩ�������D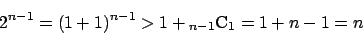
����������
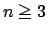 ���ے肳��C
���ے肳��C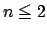 �ł��邱�Ƃ������ꂽ�D
�ł��邱�Ƃ������ꂽ�D
- 2. f(x) �̎�����
3�D�m����92�N������n�n



4�D�m���98�N�O�����n�n
��1
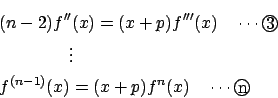
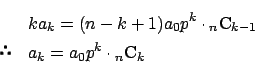
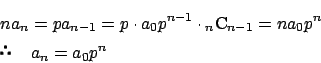
��3
�@��������![]() �ł͊�����
�ł͊�����
���ӂ� x �Őϕ�����D
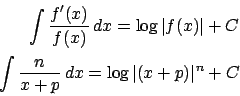
�@�������̊W����![]() �Ő�������̂�x=-p�̂Ƃ�����������.
�Ő�������̂�x=-p�̂Ƃ�����������.
�@�������̍ō������̌W���Ɣ�r���� C'=a0
5�D�m98���s�{����ȑ�n

6�D�m99���s�{����ȑ�n
- 1.
��ʂɊ� y=f(x) �̃O���t�� x=a �őΏ̂ɕϊ������O���t�̊��� y=f(2a-x) �ł���.
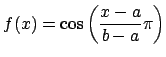 �Ƃ���.
�Ƃ���.
f(x) ��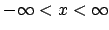 �Œ�`����
���, y=f(x) ��
�Œ�`����
���, y=f(x) ��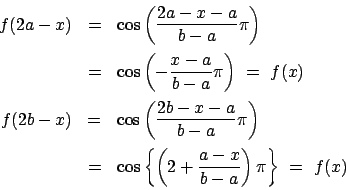
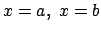 �Ɋւ��đΏ̂ł���. �����, �������݂����Ă���.
�Ɋւ��đΏ̂ł���. �����, �������݂����Ă���.
- 2. ��ӂ��
�����藧�D�Ƃ��낪, ���̂Ƃ��C�ӂ̎��� x0 �ɑ�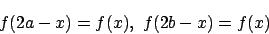 f(x0)=f(2a-x0)=f(2b-(2a-x0))=f(2b-2a+x0)�����藧�D�����������ƂȂ�. a<b ���, �����
f(x0)=f(2a-x0)=f(2b-(2a-x0))=f(2b-2a+x0)�����藧�D�����������ƂȂ�. a<b ���, �����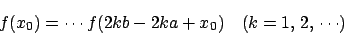 ���݂��� x �̒l�������ɂ��邱�Ƃ��Ӗ�����.
���݂��� x �̒l�������ɂ��邱�Ƃ��Ӗ�����.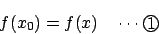
f(x) �������ł��邩��, 1�͍P�����ł���. �܂�, f(x) �͒萔�ł���. - 2. ��ӂ��
7�D�m99���s�{����ȑ�n
![]()
�@���������āC���ׂĂ� x �ɑ��˂� f(-x)=f(x) , �܂� f(x) �͋���ł���.
����
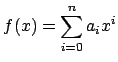 �Ƃ����
f(x)=f(-x) ���
�Ƃ����
f(x)=f(-x) ���
![]() .
.
�����,
x �̐��� F(x) ��p����
f(x)=F(x2) , ���l��, x�̐��� G(x)
��p����
g(x)=G(x2) �Ƃ�����.
![]() ���
���
�@���炩�� G(1-x) �� G(x) �̎����͓������̂� F(x) �� G(x) �̎�����������.
�@���������� f(x) �� g(x) �̎�����������.
9�D�m00�����̐����q�����n
��1
�@f(x) ��
![]() ���C
���C
![]() �� m ���Ƃ�
�� m ���Ƃ�
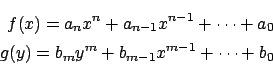
������ f(x) �� g(y) �őΏ̂Ȃ̂� ![]() �Ƃ���D
�Ƃ���D
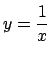 �̂Ƃ�������
�̂Ƃ�������
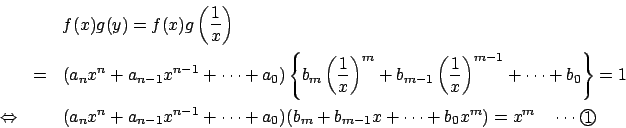
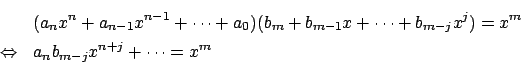
���̂Ƃ� ![]() ���
���
�䂦��
��2
�@�w�ʉ������x�u�����̐����_�v�u06����00������v�@�̍ŏI����