![]() 以下の任意の整式
以下の任意の整式 ![]() に対して,
に対して,
を満たす
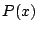 は定数倍を除いて一つしかないことを示せ.
つまり,
は定数倍を除いて一つしかないことを示せ.
つまり,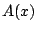 ,
,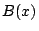 がこのような整式とすると,適当な数
がこのような整式とすると,適当な数 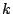 が存在して,
が存在して,
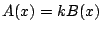 と表されることを示せ.
と表されることを示せ.
- 条件
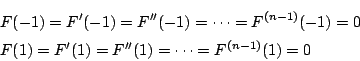
を満たす整式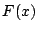 は,
は,
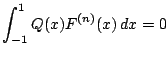 を満たす.
を満たす.
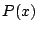 はある定数
はある定数 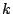 を用いて
を用いて
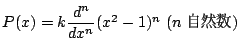 と表される.
と表される.
本問以下では
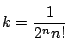 にとったものを
にとったものを 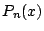 とする.
とする.
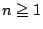 に対して,つねに
に対して,つねに
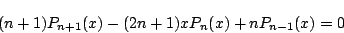
が成り立つことを示せ.-
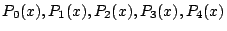 を求めよ.
を求めよ.
-
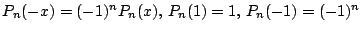 を示せ.
を示せ.
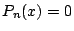 の根はすべて実数で,
の根はすべて実数で,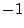 と
と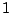 の間にあり,重解ではなく,
の間にあり,重解ではなく,
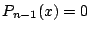 の根で分離されることを示せ.つまり
の根で分離されることを示せ.つまり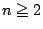 に対して,
に対して,
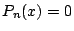 の根を小さい方から
の根を小さい方から
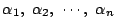 ,
,
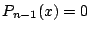 の根を小さい方から
の根を小さい方から
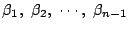 とすれば,
とすれば,
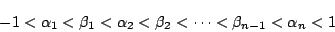
となることを示せ.- 最高次数の係数が
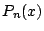 と一致する任意の
と一致する任意の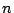 次多項式
次多項式 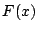 に対し,
次の不等式を示せ.
に対し,
次の不等式を示せ.
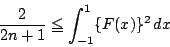
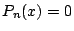 の根を
の根を
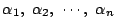 とする.
とする.
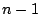 次以下の任意の整式
次以下の任意の整式 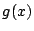 に対し,つねに,
に対し,つねに,
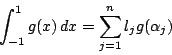
となる定数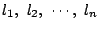 が存在することを示せ.
が存在することを示せ.
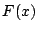 を
を 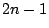 次以下の整式とするとき,
次以下の整式とするとき,
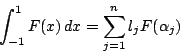
となることを示せ.