

 次: 諸命題の証明
上: 証明の試み
前: 複素平面の方法
次: 諸命題の証明
上: 証明の試み
前: 複素平面の方法
定義 3 (重心座標)
平面上に
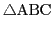
をとる.
実数の組
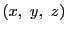
に対して
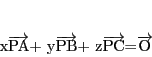 |
(2.1) |
で点
を定める.この等式は
となり
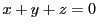
なら点
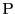
は定まらない.
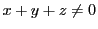
なら点
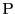
は
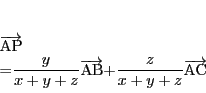 |
(2.2) |
と一意に定まる.
0でない実数
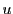
に対し
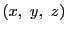
と
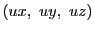
は同じ点を定める.
逆に平面上の任意の点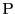 に対して,
に対して,
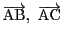 が一次独立であることより
が一次独立であることより
となる
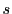
と
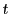
が一意に定まり,これから
となる.また0でない実数
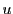
によって
とおくと,等式(
2.1)が成り立ち
となり同じ点
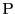
を定める.
このように
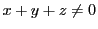
である数の組
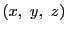
と,
平面上の点が対応する.
任意の基準点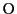 をとって等式(2.1)を書き直すと
をとって等式(2.1)を書き直すと
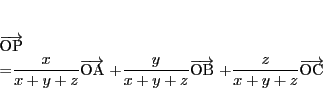 |
(2.3) |
となる.等式(
2.1)またはそれと同等な等式(
2.3)
の
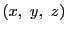
は座標系になる.
この座標系を
で定まる
重心座標系,
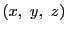
を点
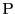
の
重心座標という.
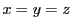 のとき点
のとき点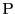 が重心となることからこの名がある.
が重心となることからこの名がある.
また,
一方
とおくと
となる.
和が1になるようにとった
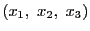 を絶対重心座標ということもある.
を絶対重心座標ということもある.
定義 4 (三線座標)
平面上に
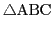
をとる.
平面上の点
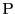
から
各辺
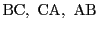
,
またはその延長上に下ろした垂線の長さの比を
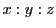
とする.
ただし,内心と点
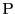
がその辺直線に関して同じ側にあるときは正,逆の側にあるときは負にとるものとする.
点
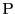
は比
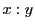
で上にあるべき直線が決まり,
その結果,比
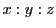
で点
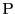
は一意に確定する.
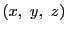
を点
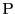
の
三線座標という.
0でない実数
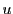
に関して,
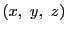
と
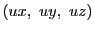
は同じ点を定める.
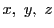
が長さそのもののときこれを
絶対三線座標という.
ここで
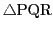 の面積を三点
の面積を三点
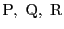 が反時計回りに配置されているとき正,一直線上にあるとき0,逆方向にあるとき負,と定める.
が反時計回りに配置されているとき正,一直線上にあるとき0,逆方向にあるとき負,と定める.
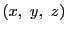 が点
が点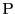 の絶対三線座標であるとき,
の絶対三線座標であるとき,
となる.よって
である.
三線座標の方法はユークリッド幾何の諸性質を解明するのに有効である.
定義そのものがユークリッド平面に依拠している.
それに対して重心座標は射影幾何的にとらえることができる.
射影平面の射影座標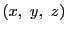 では任意の直線を無限遠直線に指定できる.
等式(2.1)で点
では任意の直線を無限遠直線に指定できる.
等式(2.1)で点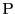 を定める座標
を定める座標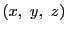 では,
では,
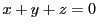 が無限遠直線であり,
が無限遠直線であり,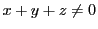 の部分がユークリッド平面になる.
の部分がユークリッド平面になる.
ユークリッド平面においては一方から他方への変換も明確である.
ここでは重心座標によってパスカルの定理を証明しよう.
座標というからには,成分間の関係式をみたす点の集合がどのような図形になるか,
ここを考えなければならない.
重心座標での方程式がわかれば三線座標での方程式もわかる.
直線は通る点と方向を与えることで定まる.
通る点を
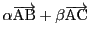 ,
方向を
,
方向を
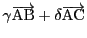 とする.
直線上の点
とする.
直線上の点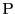 は
は
と表される.これから
となる.よって重心座標で点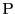 を
を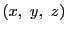 とすると,
とすると,
となる.これから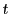 を消去して
を消去して
を得る.これを整理して
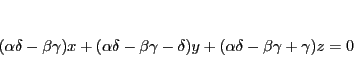 |
(2.4) |
を得る.逆に,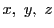 の1次同次式
の1次同次式
が与えられれば
となるように,第2,3式から
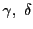 を定め
第1式から
を定め
第1式から
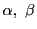 を定まった比になるようにとれば,
直線のベクトル方程式が定まる.
を定まった比になるようにとれば,
直線のベクトル方程式が定まる.
よって直線の方程式は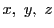 の1次同次式である.
の1次同次式である.
命題 4
で定まる二点
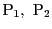
を通る直線の方程式は
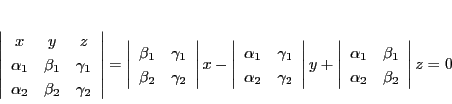 |
(2.5) |
である.
■
証明
直線の方程式(2.4)に
を代入する.代入して整理すると
つまり方程式(2.5)を得る.
□
これはまた3点
が共線である条件でもある.
円錐曲線の射影幾何での定義はのちにおこなう予定である.
ここでは,射影平面で同次二次式で定まる点の集合を円錐曲線と定める.
いいかえると
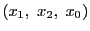 を射影座標とするとき,
を射影座標とするとき,
で定まる射影平面上の点の集合を円錐曲線という.これは行列を用いて
と表すことができる.
この円錐曲線は,重心座標ではどのような方程式で表されるのか.
これを明示的に表すために,
 ,
,
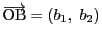 ,
,
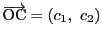 とする.
重心座標が
とする.
重心座標が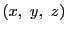 の点は直交ユークリッド座標では
の点は直交ユークリッド座標では
で表される.したがってこれを射影平面におくと
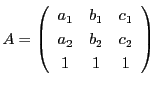 とすると,
とすると,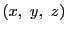 のみたすべき方程式は
のみたすべき方程式は
となり,やはり2次の同次式である.
これを整理し改めて係数を取りなおし,
重心座標による円錐曲線を
とおく.これが
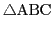 の頂点を通ることを考える.
頂点の重心座標は
の頂点を通ることを考える.
頂点の重心座標は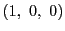 ,
,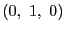 ,
,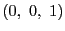 である.
これらが方程式を満たすので,
である.
これらが方程式を満たすので,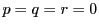 である.よって
である.よって
これが,3頂点を通る円錐曲線である.
これをもとに,
まず
 の3頂点を通る円の方程式を重心座標で表そう.
の3頂点を通る円の方程式を重心座標で表そう.
命題 5
の頂点
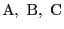
の対辺の長さを
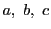
とする.
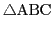
の外接円の重心座標による方程式は
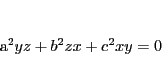 |
(2.6) |
である.
■
証明
方程式(2.6)が円錐曲線であることはわかっているので,
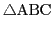 の外接円周上の点がこの方程式を満たすことを示せば,
方程式(2.6)が外接円の方程式である.
の外接円周上の点がこの方程式を満たすことを示せば,
方程式(2.6)が外接円の方程式である.
 外接円周上に点
外接円周上に点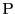 をとる.図のように弧
をとる.図のように弧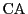 上にあるとする.
このとき円周角の定理から
上にあるとする.
このとき円周角の定理から
である.よって外接円の半径を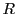 とすると
とすると
トレミーの定理から
なので,点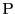 の重心座標は方程式(2.6)をみたす.
円周上の他の位置にあっても同じなので,
円周上の点はすべて方程式(2.6)をみたし,
この結果方程式(2.6)が外接円の方程式である.
□
の重心座標は方程式(2.6)をみたす.
円周上の他の位置にあっても同じなので,
円周上の点はすべて方程式(2.6)をみたし,
この結果方程式(2.6)が外接円の方程式である.
□
以上の準備の下でパスカルの定理を重心座標を用いて証明しよう.
3次行列の行列式は,2次の場合と同様に考えればよい.
 命題 6
円錐曲線
命題 6
円錐曲線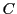 の周上に6点,A,B,C,D,E,F がこの順に並んでいる.
直線ABとDEの交点をP,
直線BCとEFの交点をQ,
直線CDとFAの交点をR
とする.このとき
の周上に6点,A,B,C,D,E,F がこの順に並んでいる.
直線ABとDEの交点をP,
直線BCとEFの交点をQ,
直線CDとFAの交点をR
とする.このとき
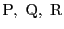 は共線である.
■
は共線である.
■
証明
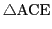 の重心座標で考える.
頂点の重心座標はそれぞれ
の重心座標で考える.
頂点の重心座標はそれぞれ
である.
円錐曲線は
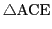 に外接しているので,その方程式は
に外接しているので,その方程式は
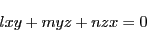 |
(2.7) |
とおける.他の3点B,D,Fの重心座標を
とおく.これらの点が方程式(2.7)をみたすので,
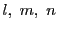 はすべてが0ではないので,
はすべてが0ではないので,
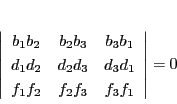 |
(2.8) |
である.二点
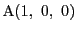 ,
,
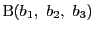 を通る直線の方程式と,
二点
を通る直線の方程式と,
二点
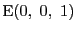 ,
,
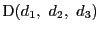 を通る直線の方程式は,それぞれ命題4より,
を通る直線の方程式は,それぞれ命題4より,
この交点を求める.これより
なのでABとDEの交点Pの重心座標は
同様にして,
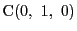 ,
,
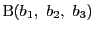 を通る直線の方程式と,
を通る直線の方程式と,
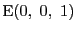 ,
,
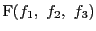 を通る直線の方程式から
BCとEFの交点Qを求めると
を通る直線の方程式から
BCとEFの交点Qを求めると
また
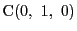 ,
,
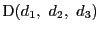 を通る直線の方程式と,
を通る直線の方程式と,
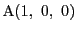 ,
,
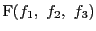 を通る直線の方程式から
CDとAFの交点Rを求めると
を通る直線の方程式から
CDとAFの交点Rを求めると
となる.この3点の共線条件を調べる.
ところがこれは
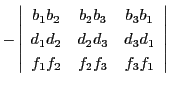 なので,等式(2.8)より値は0,つまり3点P,Q,R は共線である.
□
なので,等式(2.8)より値は0,つまり3点P,Q,R は共線である.
□
重心座標の方法は,ベクトルを用いており,それ自体は射影幾何の方法ではない.
しかし,射影幾何の基礎を作ることで,重心座標による証明を射影幾何での証明に転化することができる.それは後に行う.本質的に用いたのは三角形の頂点を基準とするある種の同次座標である.これが他の道筋で定義できるのなら,証明をもういちど生かすことは可能である.今後の課題である.


 次: 諸命題の証明
上: 証明の試み
前: 複素平面の方法
2014-01-03
次: 諸命題の証明
上: 証明の試み
前: 複素平面の方法
2014-01-03
![]() に対して,
に対して,
![]() が一次独立であることより
が一次独立であることより
![]() をとって等式(2.1)を書き直すと
をとって等式(2.1)を書き直すと
![]() に対して,
に対して,
![]() が一次独立であることより
が一次独立であることより
![]() をとって等式(2.1)を書き直すと
をとって等式(2.1)を書き直すと
![]() のとき点
のとき点![]() が重心となることからこの名がある.
が重心となることからこの名がある.
![]() の面積を三点
の面積を三点
![]() が反時計回りに配置されているとき正,一直線上にあるとき0,逆方向にあるとき負,と定める.
が反時計回りに配置されているとき正,一直線上にあるとき0,逆方向にあるとき負,と定める.
![]() が点
が点![]() の絶対三線座標であるとき,
の絶対三線座標であるとき,
![]() では任意の直線を無限遠直線に指定できる.
等式(2.1)で点
では任意の直線を無限遠直線に指定できる.
等式(2.1)で点![]() を定める座標
を定める座標![]() では,
では,
![]() が無限遠直線であり,
が無限遠直線であり,![]() の部分がユークリッド平面になる.
の部分がユークリッド平面になる.
![]() の1次同次式である.
の1次同次式である.
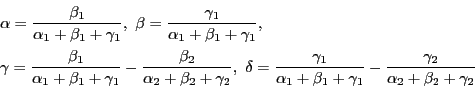
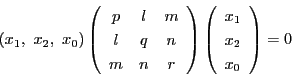
![]() ,
,
![]() ,
,
![]() とする.
重心座標が
とする.
重心座標が![]() の点は直交ユークリッド座標では
の点は直交ユークリッド座標では
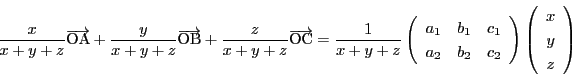
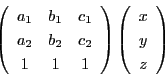
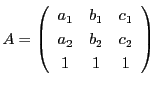 とすると,
とすると,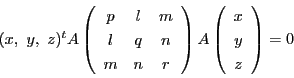
 外接円周上に点
外接円周上に点![]() をとる.図のように弧
をとる.図のように弧![]() 上にあるとする.
このとき円周角の定理から
上にあるとする.
このとき円周角の定理から
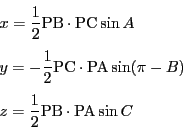
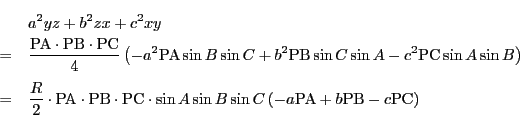
 命題 6
円錐曲線
命題 6
円錐曲線![]() の周上に6点,A,B,C,D,E,F がこの順に並んでいる.
直線ABとDEの交点をP,
直線BCとEFの交点をQ,
直線CDとFAの交点をR
とする.このとき
の周上に6点,A,B,C,D,E,F がこの順に並んでいる.
直線ABとDEの交点をP,
直線BCとEFの交点をQ,
直線CDとFAの交点をR
とする.このとき
![]() は共線である.
■
は共線である.
■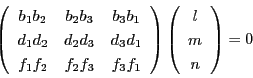
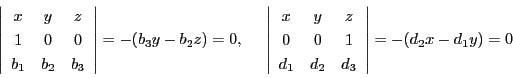
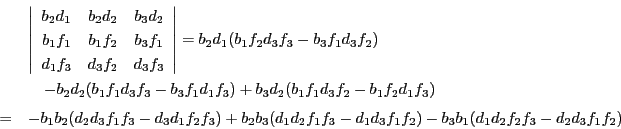
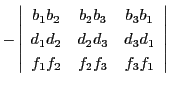 なので,等式(2.8)より値は0,つまり3点P,Q,R は共線である.
□
なので,等式(2.8)より値は0,つまり3点P,Q,R は共線である.
□