次: 神秘六角形 上: 読解 前: 読解

本文読解

定義I

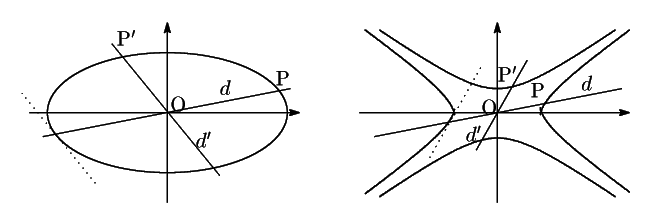
パスカルは「いくつかの直線が同じ点で交わるか，またはすべてたがいに平行であるとき，これらの直線は同じ束をなす」という．そしてこの束をなす直線の集合を線束という．デザルグの先行した研究を受けてのことであるが，パスカルは平行な場合を別に扱っていない．平行な2直線は「無限遠点で交わる」という射影幾何がすでに形づくられている．

「無限遠点」という考え方は単に頭の中で考えただけのようであるが，じつはそれを自然に含む幾何が実在することをデザルグがつかみ，そのもとで円錐曲線を考えることが円錐曲線の理解のうえでも本質的に重要であることをパスカルが見ぬいた．しかし2人によってきり拓かれた射影幾何は，その後ながく関心をひかなかった．フランス革命の頃，ようやくモンジュによって再び取りあげられ，19世紀なり射影幾何の構造が解明され，それを記述する方法も整理された．

定義II

円錐を平面で切断することによって円錐曲線が得られることは今日広く知られている．日本の高等学校の教科書では「二次曲線は，空間における円錐を，その頂点を通らない平面で切った切り口の曲線として現れることが知られている」と書かれている．

円錐曲線の研究はギリシアにはじまった．円錐曲線を系統的に研究した最初の人は，プラトンの友人であったメナイクモス(Menaechmus，B.C.350頃)であろうといわれている．メナイクモスはもちろんその後長い間，ギリシア人は円錐曲線を調べるのに，円錐をえがき，それを平面で切って考えてきた．小アジアの都市ベルガのアポロニウス(Apollonios，B.C.260〜200頃)は平面曲線として円，双曲線，楕円を定義し，今日知られている多くの性質をすでに証明した．

アポロニウスの円錐曲線論はウェブサイト『円錐曲線（題材：アポロニウスの「円錐曲線論」）』で日本語で読める．訳とそのすべてに図を与える労作である．

アポロニウスは底面と切断平面を固定し，円錐の軸を変化させてさまざまの円錐曲線を作る．これに対してデザルグは直円錐を固定し，切断平面を動かして円錐曲線を作る．アポロニウスからデザルグにおいて，円錐を動かすことから切断平面を動かすことへの転換があった．

定義IIは古い時代の円錐曲線ではなく，新しいデザルグの方法に立脚することを述べている．この観点があってはじめて，円での証明を円錐曲線に一般化するパスカルの発見がありえた．

順次，パスカルが何を言っているのか，それぞれの内容をつかんでゆこう．

補題I

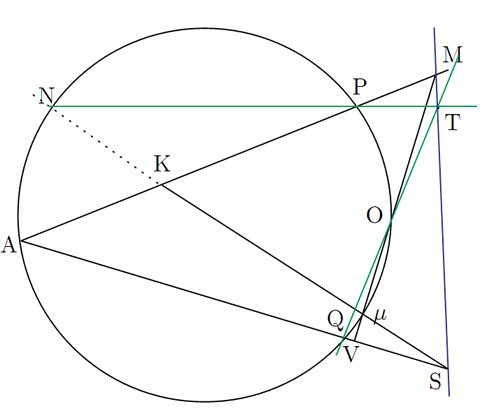補題Iは円に関するものである．補題Iでは「 4点A，K，$\mu$，Vのうちの2点でMやSとあわせた3点が同一直線上にないもの，例えばK，Vをとり」と書かれているが，これに替えてAと$\mu$をとるとどのようになるのか．図を描いてみると，この変更に応じて3直線MS，NP，OQが同じ束をなす．この共通の交点をTとおこう．

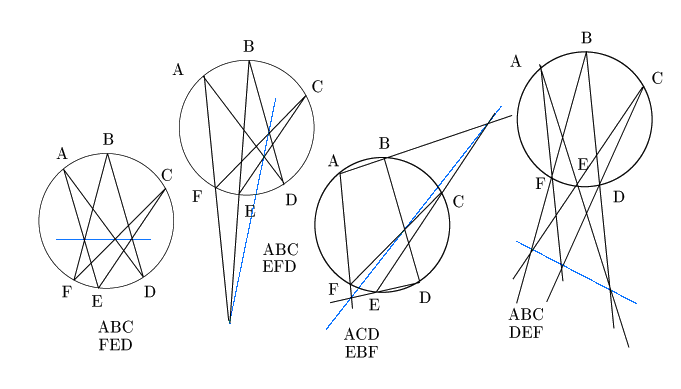
これを観点を変えてみる．つまり先に円周上の6点を考える．図4の場合は円周上に6点K，Q，V，N，O，Pがあり，図11の場合は円周上に6点N，A，Q，$\mu$，O，Pがある．

これら6点を仮にある六角形の頂点になるように配置したとき，3組の対辺ができる． それら対辺の3つの交点が同一直線上にある． 図11ではM，S，T がその3交点である．

つまり，図11では6点を六角形の頂点に

$$\begin{array}{ccccccc} &&\mathrm{N}&―&\mathrm{P}\\ ... ... &＼&&&&／&\\ &&\mathrm{O}&―&\mathrm{Q} \end{array}$$

と配置したとき，この配置で対辺にある2直線が3組みできるが，それらの3つの交点が同一線上にあることを主張している．この場合，NPとOQの交点T，APとO$\mu$の交点M，N$\mu$とAQの交点Sが同一直線上にあることである．これが六角形の頂点への他の配置でもつねに成りたつ．

円周上に6点が与えられたとき，これを仮に六角形に配置する方法は，順列と組合せで定まるだけある．六角形に配置して対辺を結ぶということは，6個の点のそれぞれが，他のちょうど2点と結ばれるようにするということと同じである．

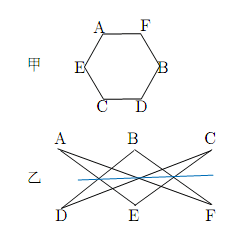6点を図の甲のように六角形に配置してその対辺の交点をとる．直線とその交点のとり方を六角形をかいて指示するのも一つの方法であるが，本書では次のように，「型」で指示する．型 $$\mathrm{A}\mathrm{B}\mathrm{C}\atop\displaystyle \mathrm{D}\mathrm{E}\mathrm{F}$$と書いて図の乙のように3個の交点をとるものとし，この型によって，6点からどのように「ちょうど2点と結ばれるようにする」かを指示することとしよう，図の乙のように点が配置できることと，六角形に配置して対辺を組みあわせることは一対一に対応している．

また $$\mathrm{A}\mathrm{B}\atop \displaystyle \mathrm{D}\mathrm{E}$$で直線$\mathrm{AE}$と直線$\mathrm{BD}$の交点を表す．これはまた $\mathrm{AE}\wedge \mathrm{BD}$とも記す．

この記号を用いるとパスカルは次の事実が成りたつことを主張している．これが円の場合のパスカルの定理である．この証明をパスカルはデザルグの方法で示したのだろう．それを垣間見る証明を後に「複比の方法」のなかでおこなう．

今後用いる新しい言葉を定義する．

定義 1        3個以上の点が同一直線上にあることを共線であるという．また3個以上の直線が一点で交わることを共点であるという． ■

これを用いると，補題1は次のようにいいかえることができる．

命題 1        円周上に6点A，B，C，D，E，Fがある．6点を $$\mathrm{X}\mathrm{Y}\mathrm{Z}\atop\displaystyle \mathrm{U}\mathrm{V}\mathrm{W}$$の型に配置する．この型で定まる3点は共線である． ■

いくつかの例をあげる．

上にあげたのはいずれも，六角形の対辺となる2直線が交点をもつ場合であった．

それに対して， $$\mathrm{A}\mathrm{B}\mathrm{C}\atop\displaystyle \mathrm{E}\mathrm{F}\mathrm{D}$$で $\mathrm{A}\mathrm{F}$と $\mathrm{B}\mathrm{E}$が平行な場合， この2直線と二つの交点を結ぶ直線$l$が線束をなすということは， これら平行2直線と$l$が平行である，ということである．

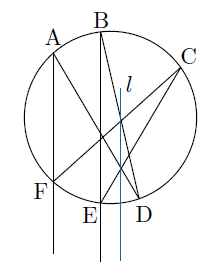パスカルは，線束という概念を平行な直線集合を含めて定義し，「線束をなす」という中に平行な場合を含めた．この意味で補題Iは例外なくすべての場合を含めた命題となっている． これはまた，AFとBEは無限遠点で交わり， $\mathrm{BD}\wedge \mathrm{CF}$と AD∧CEを通る直線も同じ無限遠点を通る，といいかえることが出来る．

あるいはそのようにいいかえることが出来る立場をこれから構築する．つまり平行な場合を例外としない立場，あるいは同じことだが無限遠点を有限点と同じように扱える立場を確立し，円錐曲線の一般的研究をすることが課題である．

補題II と第III補題

補題IIはいわゆるユークリッド空間の平面と平面の交わり図形として考えるかぎり自明である．しかし，無限遠点を例外としない立場でそのような直観が許されるのか．それも今後の問題である．

このことと，デザルグが発見しパスカルがそれを受け継いだ，円錐曲線を円錐を平面で切断する方法とを結びつけると，補題1が任意の円錐曲線で成りたつというのである．これが補題IIとそこから帰結する第IIIの補題である．

楕円とその周上の4点A，B，C，Dに対し，それをある底面が円の直円錐上に置く．円錐の頂点をOとする．これを実現する円錐の存在を示さなければならない．

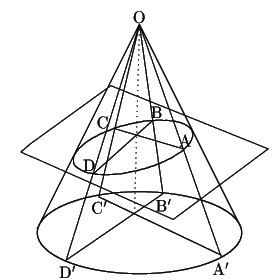OA，OB，OC，ODと底面の交点をA$'$，B$'$，C$'$，D$'$とする．すると，楕円のある平面上の2直線ACとBDが交わるかどうかは，A$'$C$'$，B$'$D$'$が交わるかどうかの問題に帰結する． 他の点もあるときこれら交点が同一直線上にあるかという問題も，すべて対応する底円上の点や交点に関して示せばよいことになる．

かくしてパスカルの定理が確立する．ただし今は「2直線が平行である」という命題を「2直線が無限遠点で交わる」で置きかえうる理論ができるものとして，パスカルの定理を述べる．

3個以上の直線が互いに平行であるとき，これらはある一つの無限遠点で交わると考えるのである．このように考えれば，直線の集合が共点であることと，パスカルの意味で束をなすことは同値である．

この考察を経て，パスカルの定理は次のような円錐曲線に関する定理に一般化される．

定理 1 (パスカルの定理)        円錐曲線上に6点A，B，C，D，E，Fがある． 6点を $$\mathrm{X}\mathrm{Y}\mathrm{Z}\atop\displaystyle \mathrm{U}\mathrm{V}\mathrm{W}$$の型に配置する．この型で定まる3点は共線である． ■

これがパスカルの定理である．パスカルは，円錐曲線に内接する六角形を神秘六角形と呼んだ．この第III補題にもとづいて，パスカルは400個の命題を証明し，円錐曲線の全理論を作ったと言われている．それが補題IIに続いて今後の予定として書かれていることである．しかし，この試論を除いて，それらの論文はそのごく一部以外は失われている．

パスカルは存命中にパリを訪れたライプニッツに会い稿本を渡している．そこにはパスカルの定理をはじめ．これら諸命題の証明があり，ライプニッツはこれを賞賛していた．ライプニッツはパスカルの死後14年の1676年に，その頃はまだ存在していたパスカルの諸原稿を整理している．それらからある程度は体系がどのようなものであったかをうかがうことはできる．『パスカル全集　第一巻』[36]の「数学論文集，解説」でパスカルの原著を読んでいたライプニッツの書簡などをもとに，その内容が追跡されている．しかし，証明そのものの詳細はわからない．

命題I

命題Iを書き換えると次のようになる．

$$\dfrac{\mathrm{MP}}{\mathrm{MA}}\cdot\dfrac{\mathrm{LA}}{\m... ...mathrm{SQ}}{\mathrm{SA}}\cdot\dfrac{\mathrm{TA}}{\mathrm{TQ}}$$

一般に直線上の4点A，B，C，Dに対して，直線のいずれかの方向を正とし，逆方向を負として，線分の長さを向きつきで考えるとき，

$$\dfrac{\mathrm{AC}}{\mathrm{AD}}\cdot\dfrac{\mathrm{BD}}{\mathrm{BC}}$$

を複比といい， $(\mathrm{A},\mathrm{B};\mathrm{C},\mathrm{D})$と表す．複比は次々節で定義し直す．この記号を用いると命題Iは

$$(\mathrm{M},\mathrm{L}\ ;\mathrm{P},\mathrm{A})= (\mathrm{S},\mathrm{T}\ ;\mathrm{Q},\mathrm{A})$$

と表される．

命題II,III

命題IIの前半は，複比の性質といわゆるメネラウスの定理から得られる．命題IIの後半，命題IIIも順次得られる．ただしこれらは円の場合には簡明であるが，それを円錐曲線に一般化するとき，問題が提起される．円の場合の証明とこれらの問題は次々節に述べる．

命題IV

これは，1639年にデザルグが見出した定理である．これは複比の相等

$$(\mathrm{Z},\delta;\psi,\mathrm{R})= (y,x;\mathrm{R},\psi)$$

を意味し，それから2点ずつの組

$$(\mathrm{R},\psi),\ (\mathrm{Z},\ y),\ (\delta,x)$$

がそれぞれ射影幾何で定義される対合関係にあることを示す定理である． それから逆に考えると，ここでパスカルの等式は

$$\dfrac{\mathrm{ZR}\cdot \mathrm{yR}}{\mathrm{Z}\psi\cdot \m... ... \mathrm{R}\cdot \mathrm{xR}}{\delta\psi\cdot \mathrm{x}\psi}$$

でなければならず，タトン が指摘しているとおり，ここにはパスカルの書き誤りがあると思われる．円での証明を次々節でおこなう．

命題V

命題5は中心のある円錐曲線，つまり楕円と双曲線に関する定理である．中心をもつ円錐曲線を有心円錐曲線という.さて，命題Vのパスカルの記述には少し勘違いがあるようである．それを読み解こう．

有心円錐曲線の中心を通る直線を直径という．有心円錐曲線は直交座標では原点を中心Oにとり，座標を選ぶことで

$$\dfrac{x^2}{a^2}\pm \dfrac{y^2}{b^2}=1\quad ＋:楕円，―:双曲線$$

と表される．双曲線の場合 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=-1$となるものを共役双曲線といい，これをあわせて考える．焦点の座標は，楕円で$a>b$のとき $(\pm\sqrt{a^2-b^2},\ 0)$，双曲線の場合は $(\pm\sqrt{a^2+b^2},\ 0)$である．焦点を通り，長軸に垂直な弦を有心円錐曲線の通径という．通径の長さは $\dfrac{2b^2}{a}$となる．

以下解読を楕円でおこなう．双曲線を含めた証明は次々節でおこなう．

楕円の直径$d$をとる．$d$に平行な弦の中点の軌跡はふたたび直径$d'$となる．$d'$を$d$に共役な直径という．$d$が楕円と交わる点における接線と，$d'$が平行になる．

楕円と直径$d$，$d'$の交点の一つを $\mathrm{P},\ \mathrm{P}'$とし， $\mathrm{OP}=a'$， $\mathrm{OP'}=b'$とする．また$d$と$d'$のなす角を$\omega$とする．このとき，

$${a'}^2+{b'}^2=a^2+b^2,\ \quad \bigtriangleup \mathrm{OPP'}の面積=\dfrac{ab}{2}$$

が成りたつ．

さらに$d$，$d'$上の点 $\mathrm{S},\ \mathrm{T}$を， $\mathrm{OS}=X,\ \mathrm{OT}=Y$であるようにとる．

$$\overrightarrow{\mathrm{OS}}+\overrightarrow{\mathrm{OT}}=\overrightarrow{\mathrm{OQ}}$$

とする．点$Q$がこの楕円上の点であるための条件は

$$\dfrac{x^2}{{a'}^2}+\dfrac{y^2}{{b'}^2}=1$$

である．つまりこれが$d$と$d'$を斜交軸とする斜交座標による楕円の方程式である．

以上の前提でパスカルを読みかえす．タトン の前掲文献の注を解釈すると，パスカルの時代に「図の矩形」は次のものを意味していた．

$a'>b'$のときを考える．先の斜交座標で $(\sqrt{{a'}^2-{b'}^2},\ 0)$となる点を通り$d'$に平行な弦を，この直径に関する通径とする．この長さは $\dfrac{2{b'}^2}{a'}$となる．この長さと$d$の(切りとられる部分の)長さ$2a'$の積を「図の矩形(の面積)」という．つまり$4{b'}^2$である．パスカルは次のように言おうとしたのではないか．

平面上にCを中心とする双曲線，楕円あるいは円AGEがある．直線ABが点Aでこの円錐曲線に接している．A$'$をCA$'$がCAに対する共役直径になる円錐曲線上の点とする．直径CAを引き，直線ABをCA$'$に等しくとる．またCBを引く．直線ABに平行な任意の直線，例えばDEを引く．円錐曲線をEで，直線AC，CBを点D，Fで切る．円錐曲線AGEが楕円あるいは円なら，直線DE，DFの平方の和は直線ABの平方に等しい．双曲線の場合には，同じ直線DE，DFの平方の差が直線ABの平方に等しい．

これなら，先の斜交座標による円錐曲線の方程式を示し，これを用いれば計算で示される．これも後に行う．

それにしても，座標幾何もまだ形成されていないこの時代に，いったいパスカルはどのようにしてこれらの結果を得たのだろうか．それを考えると，驚くとともに不思議な感じさえする．

次: 神秘六角形 上: 読解 前: 読解