しかし,これもまた,事象の独立を経てはじめてその意味が明確になることなのである. それは,別個の試行で定まる確率空間の積ということである.
100円硬貨と10円硬貨を投げる試行を考える.
われわれはすでに,100円硬貨を投げる試行の標本空間は,要素は2個,表と裏.
10円硬貨を投げる試行の標本空間も,要素は2個,表と裏.
それを![]() 軸と
軸と![]() 軸にとるように
軸にとるように![]() の組で考えた.
の組で考えた.
2つの集合の要素の組の全体の集合を,それらの集合の積という. これをもとにすれば,確率空間の積が考えられ,そこではじめてそれぞれの試行が独立であることをとらえることができる. それを考えてみよう.
2つの確率空間![]() と
と![]() があり,
があり,
![]() と
と![]() はそれぞれ
はそれぞれ![]() と
と![]() の事象だけで定まり,
たがいに
の事象だけで定まり,
たがいに![]() と
と![]() の事象とは無関係であるとする.
つまり,
の事象とは無関係であるとする.
つまり,![]() の
の![]() が起こったとき,
が起こったとき,
![]() ではその何れもが,
ではその何れもが,![]() で定まる確率で起こりうる,
で定まる確率で起こりうる,
![]() ,
,![]() でも同様ということである.
でも同様ということである.
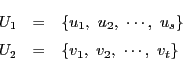
![]() と
と![]() はそれぞれ
はそれぞれ![]() と
と![]() の事象だけで定まり,
たがいに
の事象だけで定まり,
たがいに![]() と
と![]() の事象とは無関係であるとの仮定が,
埋め込みができることと同値である.
の事象とは無関係であるとの仮定が,
埋め込みができることと同値である.
任意の![]() の事象
の事象![]() と
と![]() の事象
の事象![]() に対して,
このようにして埋め込まれた
に対して,
このようにして埋め込まれた![]() の事象
の事象![]() と
と![]() は互いに独立である.
は互いに独立である.
証明
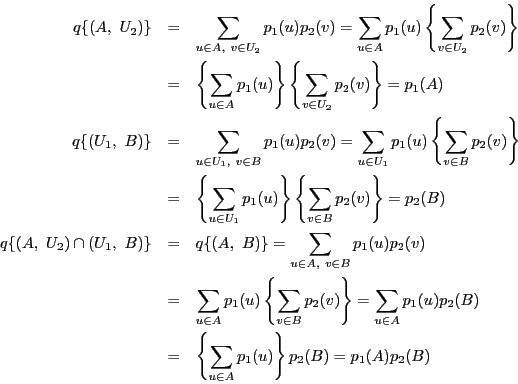
これによって
![]() の根元事象の確率が相等しく,
の根元事象の確率が相等しく,![]() の根元事象の確率も相等しく,
かつ,2つの標本空間
の根元事象の確率も相等しく,
かつ,2つの標本空間![]() と
と![]() の積集合に,事象
の積集合に,事象![]() や
や![]() が
が![]() ,
,![]() の形で埋め込めることができるとする.
の形で埋め込めることができるとする.
それぞれの事象の![]() ,
,![]() での確率は,
での確率は,
![]() ,
,
![]() である.
そして,
である.
そして,
よって標本空間![]() での事象
での事象![]() の確率は
の確率は
逆にいうと,先の![]() の確率
の確率![]() の定義は自然なものである.
の定義は自然なものである.
標本空間2個の積は,![]() 個の積にそのまま一般化される.
個の積にそのまま一般化される.