公理を立て,公理からはじめて論証を進め,新たに発見された事実を揺るぎないものとして示す,という幾何の論証はエウクレイデスにはじまる. それをまとめたものが『(幾何学)原論』である.これは複数人の共著であり, その一人がエウクレイデスであるといわれている.
エウクレイデス(Eukleides,紀元前365年〜紀元前275年,英語表記 Euclid)は古代ギリシアの数学者,天文学者とされる人で,アテナイで学びプトレマイオス1世治下のアレクサンドリアで教えた.ちなみにプトレマイオス1世とは,アレクサンドロス3世(アレキサンダー大王)の部下であったマケドニア地方出身のギリシア人で,大王の死後,エジプトの支配を継ぎ,プトレマイオス朝を創始した.
『原論』はラテン語圏,アラビア語圏にもたらされ,その後各地で二千数百年にわたって幾何学,いや数学そのもの基本となる書物であった.この書は13巻から成り,1〜6巻は平面幾何,7〜9巻は数論,10巻は無理量,11〜13巻は立体幾何を取り扱っている.
図形以外では,最大公約数を求める方法であるユークリッドの互除法,素数の個数は無限であることの背理法による証明,などが書かれている.『原論』では,概念の定義から始まり,公準(要請)・公理・命題とその作図・証明・結論という形式で書かれている. 公準とは公理のように自明ではないが,公理と同様,証明不可能な命題を意味する.近代ではこれを含めて公理とすることが一般的である.「公準」と訳されるものもここでは公理に統一する.
『原論』はこのような形式で数学を論述する.自明なことをまず明らかにし,そこからはじめて厳格な論証によって数学的現象を論述していく,この学問記述の方法は,二千年以上にわたって,数学のみならす学問一般の模範であった.いまもその精神は受け継がれるべきものである.
『原論』の原典としては例えば『ユークリッド 原論(試案)』 等にある.
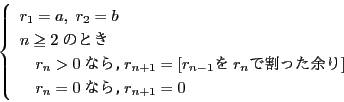
証明
(1) ![]() とすると
とすると
![]() とおける.
とおける.
これが最大公約数を求める一般的な方法で ユークリッドの互除法 といわれる.このように「必ずできる一般的方法」をアルゴリズムという.ユークリッドの互除法はアルゴリズムの基本例である.
三つ以上の整数
![]() の最大公約数もこれを応用して求めることができる.
の最大公約数もこれを応用して求めることができる.![]() が
が
![]() のなかの最小の数とする.
のなかの最小の数とする.![]() で他の数を割った余りを
で他の数を割った余りを
![]() とする.すると上の定理と同様に
とする.すると上の定理と同様に
順次割り算を行うことにより次の系列を得る.