すべての正の整数
と,0を許した四つの平方数の和として表すことができる. ■
証明 次の恒等式
![]() なら
なら ![]() で成立する.
で成立する.
![]() とする.
とする.
![]() が
が ![]() の平方剰余なら
の平方剰余なら
![]() つまり
つまり ![]() が
が ![]() の平方非剰余なら
の平方非剰余なら
![]() は
は ![]() の平方剰余
の平方剰余
![]() から始まって非剰余
から始まって非剰余 ![]() に終わる系列なので,そのなかには
に終わる系列なので,そのなかには ![]() は平方剰余で
あるが,
は平方剰余で
あるが, ![]() は非剰余であるような
は非剰余であるような ![]() が必ずある.ところがこのとき
が必ずある.ところがこのとき
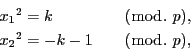
従って一般に素数 ![]() に対して
に対して
ここで ![]() なら
なら
![]() を適当な
を適当な
![]() にとりかえて
にとりかえて![]() で
で
式 (3.4) における
![]() を
を ![]() で割って絶対値最小の剰余を
で割って絶対値最小の剰余を
![]() とする.つまり
とする.つまり
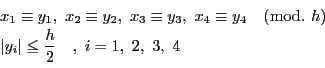
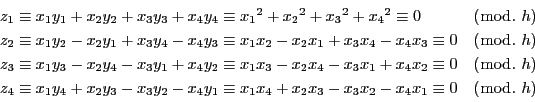
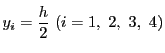 のときである.このとき
のときである.このとき