![]() から
から
![]() には下の選択肢(a),(b),(c),(d)から正しいものを選んで入れよ.
には下の選択肢(a),(b),(c),(d)から正しいものを選んで入れよ.
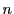 を整数とする.
を整数とする.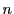 が6または15で割り切れることは,
が6または15で割り切れることは, 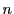 が30で割り切れるための
が30で割り切れるための
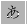 .
.
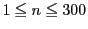 をみたし,6または15で割り切れる
をみたし,6または15で割り切れる 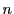 は全部で
は全部で
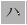 個ある.
個ある.
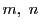 を整数とする.
を整数とする. 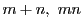 がともに12で割り切れることは,
がともに12で割り切れることは, 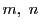 がともに6で割り切れるための
がともに6で割り切れるための
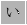 .
.
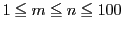 をみたし,
をみたし, 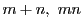 がともに12で割り切れる
がともに12で割り切れる 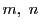 の組は全部で
の組は全部で
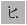 個ある.
個ある.
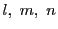 を整数とする.
を整数とする.
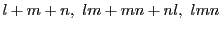 がすべて5で割り切れることは,
がすべて5で割り切れることは,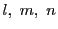 がすべて5で割り切れるための
がすべて5で割り切れるための
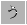 .
.
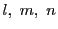 を整数とする.
を整数とする.
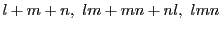 がすべて30で割り切れることは,
がすべて30で割り切れることは, 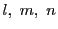 がすべて30で割り切れるための
がすべて30で割り切れるための
 .
.
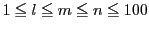 をみたし,
をみたし,
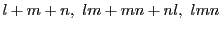 がすべて30で割り切れる
がすべて30で割り切れる 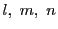 の組は全部で
の組は全部で
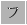 個ある.
個ある.
(a)必要十分条件である.
(b)必要条件であるが十分条件ではない.
(c)十分条件であるが必要条件ではない.
(d)必要条件でも十分条件でもない.