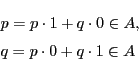このとき集合
集合![]() は差をとる演算に関して閉じている.
整数からなる集合
は差をとる演算に関して閉じている.
整数からなる集合![]() が差で閉じていれば,
ある整数
が差で閉じていれば,
ある整数![]() が存在して
が存在して
証明
条件から![]() である.
その結果,
である.
その結果,![]() なら
なら
![]() である.
また,自然数
である.
また,自然数![]() に対して
に対して![]() のとき
のとき
![]() の要素のうち正の要素からなる部分集合をとる.自然数の部分集合なので最小要素が存在する.それを
の要素のうち正の要素からなる部分集合をとる.自然数の部分集合なので最小要素が存在する.それを![]() とする.
とする.![]() の任意の要素
の任意の要素![]() をとり
をとり![]() で割る.
で割る.
逆に![]() なので,最初に示したように整数
なので,最初に示したように整数![]() に対して
に対して![]() .
つまり,
.
つまり,
![]() も成り立つ.よって
も成り立つ.よって
![]() が示された.
(証明終わり)
が示された.
(証明終わり)
この定理の証明では,自然数の部分集合には最小の要素が存在することと除法の定理がもっともカギとなるところで用いられている.
証明
(1)を示す. 整数解を![]() ,
,![]() と
と![]() の最大公約数を
の最大公約数を![]() とし,
とし,![]() とおく.
とおく.
(2)を示す.
集合![]() を
を
![]() とおく.
とおく.
![]() ,
,![]() が
が![]() に属せば
に属せば