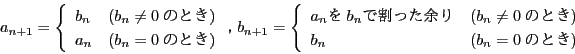正の整数 ![]() を8で割った余りを
を8で割った余りを ![]() とおく.正の整数の組
とおく.正の整数の組 ![]() は条件
は条件
をみたすとする.
- (1)
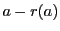 と
と 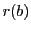 を求めよ.
を求めよ.
- (2)
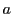 と
と 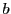 を求めよ.
を求めよ.
[10神戸文系3番]
$ a,\ b $ を自然数とする.以下の問に答えよ.
(1) $ ab $ が3の倍数であるとき,
$ a $ または $ b $ は3の倍数であることを示せ.
(2) $ a+b $ と $ ab $ がともに3の倍数であるとき,
$ a $ と $ b $ はともに3の倍数であることを示せ.
(3) $ a+b $ と $ a^2+b^2 $ がともに3の倍数であるとき,
$ a $ と $ b $ はともに3の倍数であることを示せ.
[10神戸理系2番+(0)+(4)追加]
$ p $ を3以上の素数, $ a,\ b $ を自然数とする.以下の問に答えよ.
(0) 自然数 $ m,\ n $ に対し, $ mn $ が $ p $ の倍数ならば,
$ m $ または $ n $ は $ p $ の倍数であることを示せ.
(1) $ a+b $ と $ ab $ がともに $ p $ の倍数であるとき,
$ a $ と $ b $ はともに $ p $ の倍数であることを示せ.
(2) $ a+b $ と $ a^2+b^2 $ がともに $ p $ の倍数であるとき,
$ a $ と $ b $ はともに $ p $ の倍数であることを示せ.
(3) $ a^2+b^2 $ と $ a^3+b^3 $ がともに $ p $ の倍数であるとき,
$ a $ と $ b $ はともに $ p $ の倍数であることを示せ.
(4) 自然数 $ n $ に対して $ a^n+b^n $ と $ a^{n+1}+b^{n+1} $ がともに $ p $ の倍数であるとき,
$ a $ と $ b $ はともに $ p $ の倍数であることを示せ.
二つの自然数が互いに素であるとは,二つの自然数の最大公約数が1であることをいう. 三つの自然数が互いに素であるとは,三つの自然数からどの二つの自然数を選んでも, その選んだ二つの自然数が互いに素になることをいう. このとき,次の問に答えよ.
自然数![]() について,以下の問に答えよ.
について,以下の問に答えよ.
正の整数
![]() に対して 数列
に対して 数列
![]() を次のように定義する.
を次のように定義する.
![]()
![]() について
について