next up previous 次： 体 上： 複素数の構成 前： 複素数の構成

教科書の定義

南海　 複素数の話に移ろう． 複素数はやはり何といっても難しい．しかし，複素数の発見は 人間の大きな発見だし，実数の世界の関数なども実は複素数の世界から見てこそその本質が はっきりとわかるのだ．

複素数を発見して，はじめて次のことがわかった．

  1. 代数学の基本定理

    複素数係数の $n$ 次方程式

    \begin{displaymath} x^n+a_{n-1}x^{n-1}+\cdots+a_0=0 \end{displaymath}

    は，常に $n$ 個の複素数の根をもつ．ただし， $k$ 重根は $k$ 個と数える．
  2. オイラーの等式

    2つの基本定数$\pi,\ e$ と虚数単位 $i$ の間に

    \begin{displaymath} e^{i\pi}=-1 \end{displaymath}

    が成り立つ．

(1)は，代数方程式を解くことに関しては複素数より大きい世界は要らない， ということを意味している．これまではそうではなかった． $2x+3=0$ は， 係数は整数だが，その根は整数でなく有理数だし， $x^2-2=0$ なら根は無理数だ． 実数の世界まで広げなければ根がない． このように，これまでは係数が属する世界より外の広い世界を考えなければ根がない ということが起こったが，複素数係数の代数方程式のすべて根は複素数の中に存在するので， 代数方程式を解くということでは，これより広い数の世界は要らないのだ． このことを「複素数は代数的に閉じている」という． その意味で複素数は十分に広い世界なのだ．

もちろん高校数学では，複素数を変数とする関数は， 一次分数関数 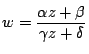$w=\dfrac{\alpha z+\beta}{\gamma z +\delta}$ や 反転 $w=\dfrac{1}{\bar{z}}$ ，あるいはせいぜい $w=z+\dfrac{a}{z}$ 以外は出てこないし， また複素数を変数とする関数の微分積分，つまり複素関数論は，もちろん習わない． 高校数学は実数の世界が中心だから，複素数が特別なものに見えるのは仕方がない面もある．

そこで例によって質問．複素数とは何か．

史織　 教科書には次のように書かれています．

平方すると $-1$ になる新しい数を一つ考えて，これを文字 $i$ で表し， 虚数単位とよぶ．すなわち

\begin{displaymath} i^2=-1 \end{displaymath}

さらに，二つの実数 $a,\ b$ を用いて

\begin{displaymath} a+bi \end{displaymath}

と表される数を考え,これを複素数という．

このようになっています．でも「新しい数を一つ考えて」と言いますが， なんかこれでは「勝手に」考えただけではないのか，勝手に作っただけではないか， 本当に虚数というのはあるのか，と感じます．

それと $bi$ と前提なしに書かれていますが，これは $b$ と $i$ をかけたものなのか， そのかけ算とはどう定義するのか，また $+$ は何と何を加えるのか，とかいろいろわかりません．

新しい数を作ったのに，その定義式に出てくる+や積はまだ定義されていない，これは変ですね．

それと「平方すると $-1$ になる数」は $\pm$ と二つあるはずなのに，どちらをとってもいいのか， ということもわかりません．

南海　 するどい！     確かに．この定義では，複素数が実在するという感じがしない． 今回は，この問題をいろいろ考えてみよう．

とりあえずこのような$a+bi$ からなる集合を $C$ と書くことにしよう． $C$ には四則計算などが成り立つ．

複素数の基本的な性質として何が書かれているか．

史織　 はい，この定義に続いて次のことが出てきます．

  1. 複素数の相等： $a+bi=c+di \Longleftrightarrow a=c,b=d$
  2. 加減法 $(a+bi)\pm(c+di)=(a \pm c)+i(b \pm d)$ (複号同順)
  3. 乗法 $(a+bi)\times(c+di)=(ac-bd)+(ad+bc)i$
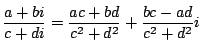
  4. 除法 $\dfrac{a+bi}{c+di}=\dfrac{ac+bd}{c^2+d^2}+\dfrac{bc-ad}{c^2+d^2}i$
  5. 共役複素数： $z=a+bi$ に対して， $a-bi$ を $z$ の共役複素数といい $\overline{z}$ と記す．

計算の仕方は，普通に $i$ を文字のようにして計算し， $i^2$ が出るたびに $-1$ に置きかえる ということです．これで確かに四則計算は実数と同じようにできます．

性質(1)(2)は2つのベクトル $(a,\ b)$ と $(c,\ d)$ の相等，加減法と同じです． しかし，(3)以降はベクトルにはないことでした．

南海　 いいところに気づいた．今したことは，複素数 $a+bi$ にベクトル $(a,\ b)$を対応づける ということだ．

史織　 でも「何かよくわからない$i$」 を用いて定義された$a+bi$ をベクトル $(a,\ b)$に対応 させるといっても，はじめの「何かよくわからない $i$」ということはいっこう変わりません．

南海　 そうだな．ここは発想を変えねばならない．

ところで質問だが， $x^2=2$ の解は何か．

史織　 $x=\pm \sqrt{2}$ です．

南海　 その$\sqrt{2}$はどんな数なのか．

史織　 2乗すると2になる正の数です．

南海　 実際にどんな数なのか．

史織　 $1.41421356\cdots$ ですが…．

南海　 それは本当に数として存在するのか． $i$ はあるのかないのか分かりにくいというが $\sqrt{2}$は大丈夫か．

史織　 でも，数直線上の目盛りを打ったこの辺りに，…．

南海　 $\sqrt{2}$が有理数でなく無理数だということは背理法で示される． が，そもそも$\sqrt{2}$が存在するのかということを厳密に示そうとすれば難しい． 19世紀になっていろいろ数学の基礎が問題になってはじめて，実数の深い性質が研究され 解明された．しかし，そのような基礎づけを知らなくても$\sqrt{2}$は存在すると確信できる． それは，実数に対して数直線というモデルがあって， 実数をその上の点としてとらえることができるからだ．

複素数もそのように具体的なモデルがあれば存在が確信できる．

史織　 それが複素数平面ですか．

南海　 結果として，複素数平面は具体物の一つなのだが， 先に「何かよくわからない $i$」を用いて複素数 $a+bi$ を定義して， それからこれに $(a,\ b)$ を対応させたのでは，はじめの複素数がわからないままになる．

そこで複素数を「何かよくわからない$i$」 からはじめるという構成を変えて， 存在が実感できるものから構成したいのだ．

ただし，構成する以上，どのようなものを作るのかはっきりしていなければならない．


Aozora Gakuen