史織 「確率変数」はどのように考えればいいのでしょうか.
南海
確率空間![]() があるとする.
があるとする.
![]() の要素である試行の結果に対して実数値が定まるとき,その実数を定める規則を確率変数という.
の要素である試行の結果に対して実数値が定まるとき,その実数を定める規則を確率変数という.
史織
![]() の要素
の要素![]() に対して実数
に対して実数![]() が定まると言うことですか.つまり
が定まると言うことですか.つまり![]() から実数への写像ですね.
から実数への写像ですね.
そうか.すると数![]() に対し
に対し![]() である確率とは,数の値が
である確率とは,数の値が![]() となるような結果の集合で定まる事象の確率だ.
となるような結果の集合で定まる事象の確率だ.
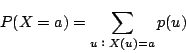
南海
そうだ.
このように特に断らなければ![]() で確率変数
で確率変数![]() が値
が値![]() をとる確率を表すことにしよう.
をとる確率を表すことにしよう.
確率変数![]() のとる値の全体が
のとる値の全体が
![]() であるとすると,
であるとすると,![]() は
値
は
値
![]() に対して確率
に対して確率
![]() を対応させる.
この対応を
を対応させる.
この対応を![]() の確率分布と言う.
の確率分布と言う.