next up previous
次： 命題と命題関数 上： 命題と命題関数 前： 命題と命題関数

教科書は何といっているか


南海　 今日は，「命題と条件」について考えよう． 「命題」を土台にして「条件」とは何かを明確にすることが目的だ．

史織　 さっそくですが．私の教科書では論証に関する記述が「必要条件と十分条件」で初めて 出てきます．その最初に次のように書かれています．

二つの事柄 $p,\ q$ に対して， $p\Rightarrow q$ がなりたつとき

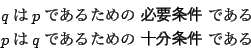
\begin{displaymath} \begin{array}{l} q は p であるための\ \textbf{必要条件}\ .. ...\ p 、マ q 、ヌ、「、・ソ、皃ホ\ \textbf{ススハャセ魴陜\ である \end{array}\end{displaymath}

という．
と書かれています．この「事柄」って何なんでしょうか．「条件」ではないのですか．

南海　 うーん．確かにこれは難しい問題だ．数学的「事柄」であるにはちがいないが． 「事柄」では少し漠然としている． 「必要『条件』」などと用いられる以上， $p$ は「条件」であるはずだ，というのはもっともだ．

具体的に考えてみよう．簡単なものでいいから例を作ってほしい．

史織　 $p$ を「16は4の倍数である」， $q$ を「16は2の倍数である」とすると，これは $p\Rightarrow q$の例になっているのでしょうか．

南海　 「事柄」というからには今あげてくれた $p$ や $q$ も事柄には違いない． 「$16=4\times 4$より $16は4の倍数\ \Rightarrow\ 4は2の倍数\ \Rightarrow\ 16 は2の倍数$」 は推論としてはあり得る．だから例には違いないのだが， $p$ も $q$ もそれ自身で真であることが確定する命題である．

事柄といえばこのようなものも入る． しかし必要条件や十分条件を考える例としては $p$ や $q$ は成立するときもしないときもあって $p$ が成立する「ならば」 $q$ が成立する，あるいはその逆に $q$ が成立する「ならば」 $p$ が成立する， というものでないと，実質的な数学上の意味がない．

そういう例をあげてほしい．

史織　 では， $p$ を「$x$は4の倍数である」， $q$ を「$x$は2の倍数である」とすると，これは $p\Rightarrow q$の例になっているのでしょうか．

南海　 そうだ．このばあい $p\Rightarrow q$は「$x$が4の倍数である，ならば，$x$は2の倍数である」 という命題になり．教科書が言いたかった例になっている．

史織　 この「$x$は4の倍数である」はやはり「事柄」というよりは「条件」ですね． でも，自分でいっておきながら何ですが，「条件」とは何ですか．

南海　 それを考えるために，まず「命題」や「真」の意味を明確にしなければならない． なぜなら，上の教科書の記述の中に，表には出されていないが，「命題」と「真」という 概念が使われている．どこに隱されているかな．

史織　 そうか． $p\Rightarrow q$が命題ですね． 「なりたつとき」とうのは「真であるとき」ですね．そうか，必要条件や十分条件とは何か を明確に述べるには，先に「命題」とか「真」とかがはっきりしていないといけないのですね．

南海　 それで，これらについて教科書はどのようにいっているか．

史織　 「命題と証明」に次のように定義されています．

式や文章で表された事柄で，正しいか正しくないかが，明確に決まるものを命題という． 命題が正しいことを真であるといい，正しくないことを偽であるという．

南海　 なるほど．「事柄」は定義されていないが，数学的現象について何らかの事実や推論を述べたもの， と言いかえてもいいだろう．

「命題」はいくらでも複雜なものがあり得るが，いちばん単純なのは， 「何々について述べる」という主題の部分(主部)と， 「何々である」とそのものの内容を述べる述語の部分(述部)から成り立っている， 断定型である．「3は奇数である」とかのたぐいだ．

これに対して $p\Rightarrow q$という形をした推論型も命題である．

もちろん「3は奇数である」は「ある数が3なら，その数は奇数である」と状況を 複雜に設定すればわかるように，断定型も掘りさげれば推論を含んでいる．

一応ここでは，命題には事実を述べた断定型と，推論を述べた推論型がある，と考えよう． のちに述べるが，推論型命題を普通は「含意命題」という．

史織　 推論型について，教科書では続いて次のように書かれています．

\begin{displaymath} n\ が奇数ならば \quad n^2-1\ は8の倍数である \end{displaymath}

のように二つの条件 $p,\ q$ を用いて

\begin{displaymath} p\ ならば\ q \quad すなわち \quad p \Rightarrow q \end{displaymath}

の形に表される命題を考えよう．

このとき， $p$ をこの命題の仮定， $q$ を結論という．
と書いてあります．

するとやはり最初の私の質問にある「事柄」は「条件」ですね．しかし肝心の「条件」とは何か， よくわかりません．


Aozora Gakuen