有限性の証明への道

次: 参考にした文献上: 存在と構成前: ユニタリー群の場合

有限性の証明への道

南海　

に関する不変式の有限性は示せた．

これをもとにに関する不変性がどのように示されるのか話そう．はいま次式としている．この場合に一般化することは難しくないので，計算は，つまりこれまでやってきた場合にしたい．

まず，が

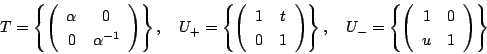
$\begin{displaymath} T=\left\{\left( \begin{array}{cc} \alpha&0\\ 0&\alpha^{-1}... ...eft( \begin{array}{cc} 1&0\\ u&1 \end{array}\right)\right\} \end{displaymath}$

という3つの部分群で生成されることは示した．ところが

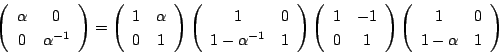
$\begin{displaymath} \left( \begin{array}{cc} \alpha&0\\ 0&\alpha^{-1} \end{ar... ...left( \begin{array}{cc} 1&0\\ 1-\alpha&1 \end{array}\right) \end{displaymath}$

のように，

の元が

と

で書けるので，

は

と

で生成される．

耕介　ということはがであるための必要十分条件は

$\begin{displaymath} Df=0,\ \Delta f=0 \end{displaymath}$

なわけですね．

南海　さて不変ならもちろん不変である．ところが方程式の不変式に関してはこの逆も成り立つ．

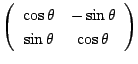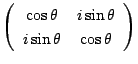には $\left( \begin{array}{cc} \cos\theta&-\sin\theta\\ \sin\theta&\cos\theta \end{array}\right)$ や $\left( \begin{array}{cc} \cos\theta&i\sin\theta\\ i\sin\theta&\cos\theta \end{array}\right)$ が含まれる．

耕介　最初のものは $\theta$ の回転ですね．

南海　まず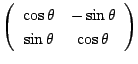， $\left( \begin{array}{cc} \cos\theta&-\sin\theta\\ \sin\theta&\cos\theta \end{array}\right)$ に対応する３次行列(6)を書いてほしい．

耕介　

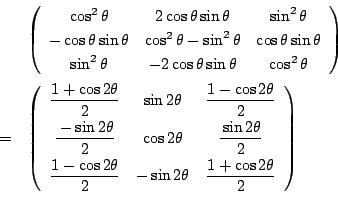
$\begin{eqnarray*} &&\left( \begin{array}{ccc} \cos^2\theta&2\cos\theta\sin\the... ...}{2}&-\sin2\theta &\dfrac{1+\cos2\theta}{2} \end{array}\right) \end{eqnarray*}$

南海　 $f(a,\ b,\ c)$ が角 $\theta$ を変化させたときに不変であることは，変換を行った式を $\theta$ で微分したとき恒等的に0になるということだった．計算してみてほしい．

耕介　

$\begin{eqnarray*} &&\dfrac{d}{d\theta}f\left( a\dfrac{1+\cos2\theta}{2}+b\sin2\t... ...uad +\left.a\sin2\theta-2b\cos2\theta-c\sin2\theta\right)f_c(〃) \end{eqnarray*}$

南海　この結果を次のように変形する．

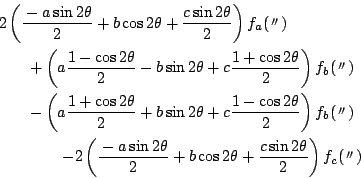
$\begin{eqnarray*} &&2\left(\dfrac{-a\sin2\theta}{2}+b\cos2\theta+\dfrac{c\sin2\t... ...in2\theta}{2}+b\cos2\theta+\dfrac{c\sin2\theta}{2}\right)f_c(〃) \end{eqnarray*}$

耕介　これが恒等的に0になることは，

$\begin{displaymath} \left( 2b\dfrac{\partial }{\partial a}+ c\dfrac{\partial }{\... ...tial b}- 2b\dfrac{\partial }{\partial c}\right)f=(\Delta-D)f=0 \end{displaymath}$

と同値です．

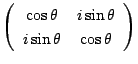南海　次に $\left( \begin{array}{cc} \cos\theta&i\sin\theta\\ i\sin\theta&\cos\theta \end{array}\right)$ に対応する３次行列(6)を書いて同様に続けてほしい．

耕介　

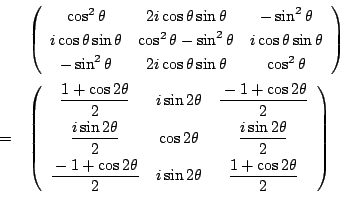
$\begin{eqnarray*} &&\left( \begin{array}{ccc} \cos^2\theta&2i\cos\theta\sin\th... ...}{2}&i\sin2\theta &\dfrac{1+\cos2\theta}{2} \end{array}\right) \end{eqnarray*}$

これを用いて同じように計算する．

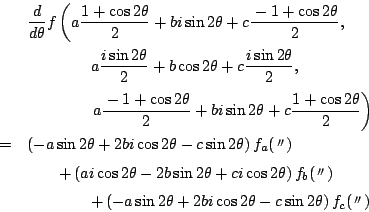
$\begin{eqnarray*} &&\dfrac{d}{d\theta}f\left( a\dfrac{1+\cos2\theta}{2}+bi\sin2\... ...d +\left(-a\sin2\theta+2bi\cos2\theta-c\sin2\theta\right)f_c(〃) \end{eqnarray*}$

この結果を次のように変形する．

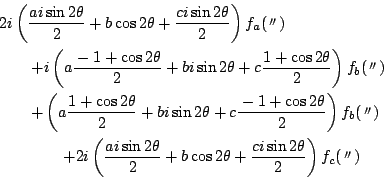
$\begin{eqnarray*} &&2i\left(\dfrac{ai\sin2\theta}{2}+b\cos2\theta+\dfrac{ci\sin2... ...n2\theta}{2}+b\cos2\theta+\dfrac{ci\sin2\theta}{2}\right)f_c(〃) \end{eqnarray*}$

これが恒等的に0になることは，

$\begin{displaymath} \left( 2bi\dfrac{\partial }{\partial a}+ ci\dfrac{\partial }... ...al b}+ 2bi\dfrac{\partial }{\partial c}\right)f=i(\Delta+D)f=0 \end{displaymath}$