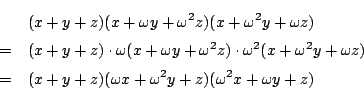次: 根と解
上: 3次方程式
前: 3次方程式
耕一
最近面白い因数分解に出会いました.それは
です.ただし,ωは1の3乗根です.
と,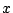 の2次方程式とみて解の公式を使うと
の2次方程式とみて解の公式を使うと
これから
は大変きれいな因数分解です.これは何か役に立つのでしょうか.
南海
右辺は見かけは 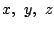 の対称式ではないが,それは大丈夫かな.
の対称式ではないが,それは大丈夫かな.
耕一 それは
のようにできるので,大丈夫です.
南海
この因数分解の左辺は三次式だがそれが右辺では一次式三つに分解されている.
これを使うと,三次方程式を一般的に解くことができる.
この機会に方程式について順に考えていこう.
Aozora Gakuen
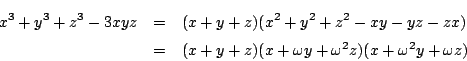
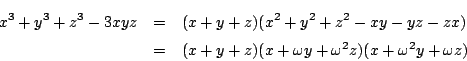
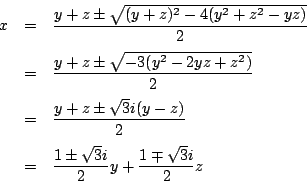
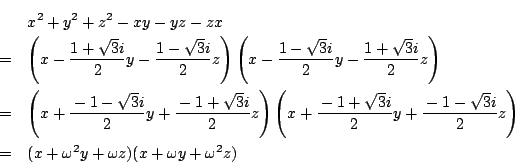
![]() の対称式ではないが,それは大丈夫かな.
の対称式ではないが,それは大丈夫かな.