- (1)
-
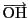 を
,
を
,
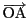 ,
,
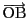 ,
,
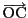 で表せ.
で表せ.
- (2)
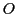 の円周上の点
の円周上の点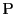 に対して,
に対して,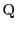 は
は
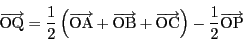
をみたす点とする.点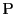 が外心
が外心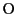 に対する
に対する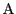 の対称点
の対称点
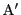 のとき,
のとき,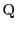 の位置を求めよ.
の位置を求めよ.
- (3)
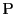 が円
が円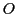 の周上を動くとき,点
の周上を動くとき,点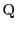 の軌跡を求めよ.
の軌跡を求めよ.
耕一
(1)の![]() は
は
![]() の垂心で,
の垂心で,
![]() となります.これは知っていました.
(2)の解は線分
となります.これは知っていました.
(2)の解は線分![]() の中点です.これも代入すればわかります.
(3)で外接円の半径を
の中点です.これも代入すればわかります.
(3)で外接円の半径を![]() とすると点
とすると点![]() のベクトル方程式は
のベクトル方程式は
![]() となる.
ここに
となる.
ここに
![]() を代入し
を代入し![]() を消去,整理して
を消去,整理して![]() のベクトル方程式をつくると
のベクトル方程式をつくると
 さらにこの問題の解説のなかで先生が,
まず鋭角三角形であることは必要でない.鈍角三角形,直角三角形でも同様に円が定まるといわれました.
確かに辺の延長線上を考えても,直交関係などは同じことなので,鈍角三角形でも同じです.
さらにこの問題の解説のなかで先生が,
まず鋭角三角形であることは必要でない.鈍角三角形,直角三角形でも同様に円が定まるといわれました.
確かに辺の延長線上を考えても,直交関係などは同じことなので,鈍角三角形でも同じです.
その上で,軌跡の円の上には,各頂点から対辺への垂線の足, 各辺の中点の合計9個の点が乗っていることを教えてくれました. 実際に図を描くと確かに9個の点が1つの円上にあって,感動しました.
各辺の中点の3点で定まる円と, 頂点から対辺への垂線の足の3点で定まる円と, 頂点と垂心の中点である3点で定まる円が一致するのです.
南海 一つの円上に9個もの点が乗っている. だからこの円を九点円というのだ. 最初にこれを見つけた人は感動しただろう.
ところが九点円はさらに不思議ないくつもの性質をもっている.
それがフォイエルバッハの定理だ.
フォイエルバッハの定理とは
![]() の内接円や傍接円がこの九点円に接しているということなのだ.
の内接円や傍接円がこの九点円に接しているということなのだ.
耕一 内接円と接しているのですか. 図を描いてみます. 接点が細かくなって少し見にくいですが, 確かに接しています.傍接円と接している方が見やすいです.

証明
点![]() を
を
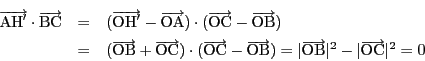
線分![]() の中点を
の中点を![]() ,
辺
,
辺![]() の中点を
の中点を![]() ,
直線
,
直線![]() と辺
と辺![]() の交点を
の交点を![]() とする.
とする.
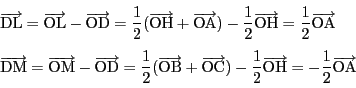

この3点の組について示されたことは, 他の3点ずつの2組についても成立する.
中心と半径はいずれも同じなので,題意の9個の点は,
点![]() を中心とする
半径
を中心とする
半径![]() の円周上に存在することが示された.
□
の円周上に存在することが示された.
□
南海 これでよい.
フォイエルバッハが1822年に証明したものである. このフォイエルバッハは『キリスト教の本質』等の著者である有名なフォイエルバッハの兄弟である. 欧州はフランス革命の後であり,今日に続く思想が生まれた時代である. この時代は日本でいえば江戸時代文政年間,幕藩体制の矛盾は大きくなっていたが,まだ討幕運動には至らないときであった.
今回はこの事実を三通りの方法で証明し,さらに接点を特徴づけていこう. 幾何の論証はこの半世紀,高校ではあまり教えられなくなった. この分野は19世紀に大きく展開され,膨大な蓄積があるが, それが受け継がれなくなっていくのはたいへん惜しい. だからできるだけ最近の高校生にわかりやすくやってみたい.