

 次: 反転法による証明
上: 九点円の不思議
前: 座標の方法による証明
次: 反転法による証明
上: 九点円の不思議
前: 座標の方法による証明
南海
古典的な平面幾何の論証による証明を紹介しよう.
 図のように
図のように
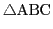 の内接円と辺BCとの接点をD,
内心をIとし,AIと辺BCとの交点をP,
また辺BCの中点を
の内接円と辺BCとの接点をD,
内心をIとし,AIと辺BCとの交点をP,
また辺BCの中点を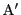 ,辺ACの中点を
,辺ACの中点を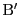 とする.
頂点Aから対辺への垂線の足をKとする.
とする.
頂点Aから対辺への垂線の足をKとする.
点Pから内接円に辺と異なる接線を引き,接点をF,PFと辺ABの交点をGとする.
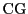 と直線AIの交点をE,直線AFと内接円の交点をLとする.
と直線AIの交点をE,直線AFと内接円の交点をLとする.
このときLは九点円上にあり,九点円と内接円はLで接している.
これを証明しよう.
必要なら点の名前をつけ替え
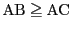 とする.
内接円と中心と通る直線APに関する対称性から
とする.
内接円と中心と通る直線APに関する対称性から
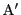 とEが線分BCと
とEが線分BCと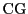 の中点であり,
の中点であり,
A,C,K,E はACを直径とする円周上の点であるから,
内接四角形ACKEの対角とその外角の関係などより
この結果,接弦定理によって,
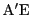 は
は
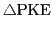 の外接円に接する.
よって方べきの定理から
の外接円に接する.
よって方べきの定理から
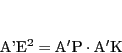 |
(3) |
ここで
であり,また内接点と辺長の関係より
なので
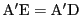 .よって(3)と方べきの定理から
.よって(3)と方べきの定理から
方べきの定理の逆からL,F,P,Kは共円である.
内接四角形LFPKの対角とその外角の関係などより
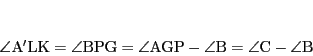 |
(4) |
ここで
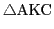 は直角三角形で
は直角三角形で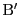 がACの中点であるから,
がACの中点であるから,
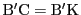 .
よって
.
よって
また
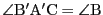 なので,
なので,
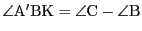 である.
である.
(4)とあわせて
である.円周角の定理から,点Lが九点円上にあることが示された.
Lにおける内接円の接線をLXとする.L,F,P,Kは共円なので
これはLXが九点円にも接することを示している.
□
耕一
すごいものですね.
円周角の定理は強力な定理です.
Aozora Gakuen
 図のように
図のように
![]() と直線AIの交点をE,直線AFと内接円の交点をLとする.
と直線AIの交点をE,直線AFと内接円の交点をLとする.
![]() とする.
内接円と中心と通る直線APに関する対称性から
とする.
内接円と中心と通る直線APに関する対称性から
![]() は直角三角形で
は直角三角形で![]() がACの中点であるから,
がACの中点であるから,
![]() .
よって
.
よって