

 次: パスカルの定理の別証明
上: 重心座標
前: 三線座標
次: パスカルの定理の別証明
上: 重心座標
前: 三線座標
太郎
座標というからには,成分間の関係式をみたす点の集合がどのような図形になるか,
ここを考えなければならないです.
重心座標での方程式がわかれば三線座標での方程式もわかる.
重心座標で考えます.
直線は通る点と方向を与えることで定まる.
通る点を
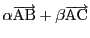 ,
方向を
,
方向を
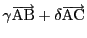 とする.
直線上の点
とする.
直線上の点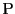 は
は
と表される.これから
となる.よって重心座標で点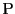 を
を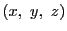 とすると,
とすると,
となる.これから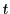 を消去して
を消去して
を得る.これを整理して
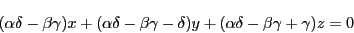 |
(6) |
を得る.逆に,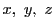 の斉次1次式
の斉次1次式
が与えられれば
となるように,第2,3式から
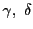 を定め
第1式から
を定め
第1式から
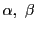 を定まった比になるようにとれば,
直線のベクトル方程式が定まる.
を定まった比になるようにとれば,
直線のベクトル方程式が定まる.
よって直線の方程式は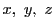 の斉次1次式である.
の斉次1次式である.
命題 1
で定まる二点
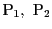
を通る直線の方程式は
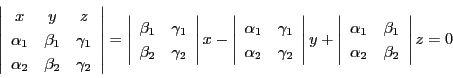 |
(7) |
である.
■
証明
直線の方程式(6)に
を代入する.代入して整理すると
つまり方程式(7)を得る.
□
これはまた3点
が共線である条件でもある.
南海
円錐曲線の射影幾何での定義は,今後『幾何学の精神』でおこなう予定である.
ここでは,射影平面で斉次二次式で定まる点の集合を円錐曲線と定める.
いいかえると
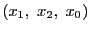 を射影座標とするとき,
を射影座標とするとき,
で定まる射影平面上の点の集合を円錐曲線という.これは行列を用いて
と表すことができる.
この円錐曲線は,重心座標ではどのような方程式で表されるのか.
これを明示的に表すために,
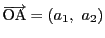 ,
,
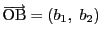 ,
,
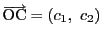 とする.
重心座標が
とする.
重心座標が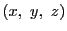 の点は直交ユークリッド座標では
の点は直交ユークリッド座標では
で表される.したがってこれを射影平面におくと
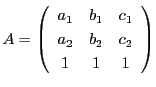 とすると,
とすると,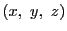 のみたすべき方程式は
のみたすべき方程式は
となり,やはり二次の斉次式である.
これを整理し改めて係数を取りなおし,
重心座標による円錐曲線を
とおく.これが
 の頂点を通ることを考える.
頂点の重心座標は
の頂点を通ることを考える.
頂点の重心座標は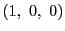 ,
,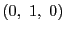 ,
,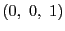 である.
これらが方程式を満たすので,
である.
これらが方程式を満たすので,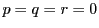 である.よって
である.よって
これが,3頂点を通る円錐曲線である.
南海
これをもとに,
まず
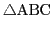 の3頂点を通る円の方程式を重心座標で表そう.
の3頂点を通る円の方程式を重心座標で表そう.
命題 2
の頂点
の対辺の長さを
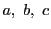
とする.
の外接円の重心座標による方程式は
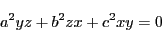 |
(8) |
である.
■
証明
方程式(8)が円錐曲線であることはわかっているので,
 の外接円周上の点がこの方程式を満たすことを示せば,
方程式(8)が外接円の方程式である.
の外接円周上の点がこの方程式を満たすことを示せば,
方程式(8)が外接円の方程式である.
 外接円周上に点
外接円周上に点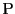 をとる.図のように弧
をとる.図のように弧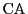 上にあるとする.
このとき円周角の定理から
上にあるとする.
このとき円周角の定理から
である.よって外接円の半径を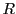 とすると
とすると
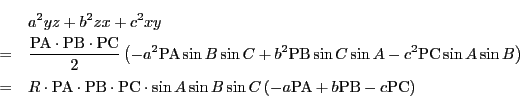
(/2を/4に訂正)
トレミーの定理から
なので,点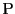 の重心座標は方程式(8)をみたす.
円周上の他の位置にあっても同じなので,
円周上の点はすべて方程式(8)をみたし,
この結果方程式(8)が外接円の方程式である.
□
の重心座標は方程式(8)をみたす.
円周上の他の位置にあっても同じなので,
円周上の点はすべて方程式(8)をみたし,
この結果方程式(8)が外接円の方程式である.
□


 次: パスカルの定理の別証明
上: 重心座標
前: 三線座標
Aozora Gakuen
次: パスカルの定理の別証明
上: 重心座標
前: 三線座標
Aozora Gakuen
![]() の斉次1次式である.
の斉次1次式である.
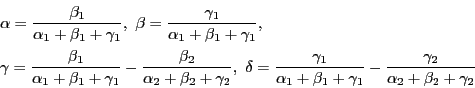
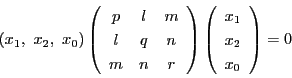
![]() ,
,
![]() ,
,
![]() とする.
重心座標が
とする.
重心座標が![]() の点は直交ユークリッド座標では
の点は直交ユークリッド座標では
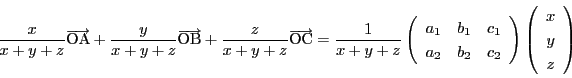
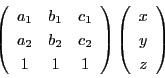
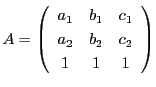 とすると,
とすると,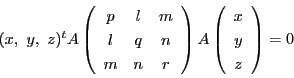
 外接円周上に点
外接円周上に点![]() をとる.図のように弧
をとる.図のように弧![]() 上にあるとする.
このとき円周角の定理から
上にあるとする.
このとき円周角の定理から
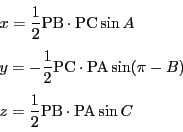
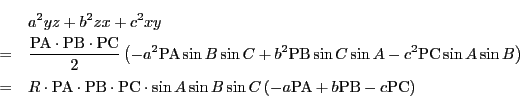 (/2を/4に訂正)
(/2を/4に訂正)