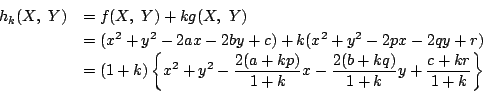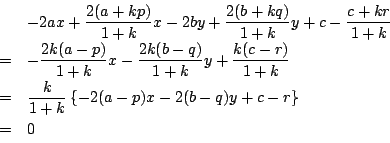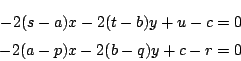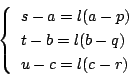次: パスカルの定理
上: 根軸
前: 曲線族と「束」
南海
その関連を解明するのが次の問題です.その疑問(2)は次の
問題の(1)で解決されます.それから逆に疑問(1)を見直す.
やってみてほしい.
定理 8
二つの二次式
拓生
証明
- 円の中心を
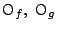 とし,円の中心と半径を求める.
とし,円の中心と半径を求める.
よって,
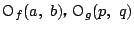 ,
半径の二乗は
,
半径の二乗は
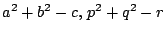 である.
である.
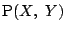 とする.
とする.
 よって点
よって点 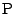 は
は
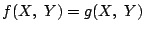 を満たす点である.つまり求める軌跡は,
を満たす点である.つまり求める軌跡は,
-
である.ここで,
である.二円 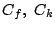 の根軸は,
二円
の根軸は,
二円 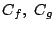 の根軸と一致する.
の根軸と一致する.
- 円
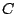 の式
の式 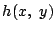 を
を
と置く.題意より二つの根軸:
が一致する.よってある実数 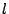 があって,
があって,
つまり
と表される.よって,
つまり 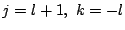 と置けばよい.□
と置けばよい.□
南海
なかなか見事なものだ.これで君の疑問はすべて解決したな.また,
二円が共有点を持つときは,その二点を通る他の円は,従って根軸が共通な円であり,問題の
(3)によって,必ずもとの二円によって,
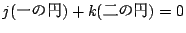 と表せる.
と表せる.
拓生
私の疑問(2)が解けました.二円の接点までの距離が等しい点の軌跡
として根軸を定義する.その根軸という考え方に立てば,二円が,二点で交わっているか,
接しているか,離れているかは,無関係なのですね.
南海 なお関連入試問題として,91年東大後期をよく考えておいてほしい.これは,2円の直行する円群は共通の根軸をもつということを意味している.
Aozora Gakuen
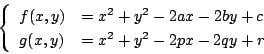
 平面の点
平面の点 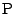 から
から 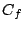 と
と 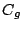 に接線を引きその接点をそれぞれ
に接線を引きその接点をそれぞれ
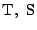 とする.
とする.
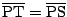 となる点
となる点 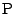 の軌跡は
の軌跡は
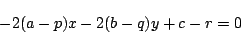
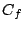 と
と 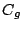 の根軸」と呼ぶ.
の根軸」と呼ぶ.
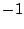 でない実数
でない実数 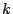 に対して,
に対して,
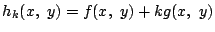 とおき,
とおき,
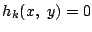 で円が定まるとき,これを
で円が定まるとき,これを 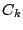 とする.二円
とする.二円 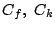 の根軸は,
二円
の根軸は,
二円 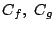 の根軸と一致する.
の根軸と一致する.
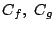 とは異なる円
とは異なる円 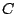 と
と 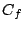 との根軸が,
二円
との根軸が,
二円 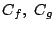 の根軸と一致したとする.このとき円
の根軸と一致したとする.このとき円 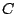 の式はある実数
の式はある実数 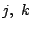 によって
によって
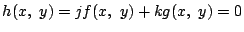 と表される.
と表される.
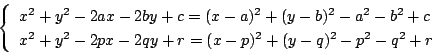
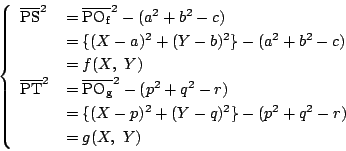
 よって点
よって点