南海 次の凸関数だ.凸関数の定義そのものは次のようになる.
関数 ![]() が定義域で「凸である」とは,定義域内の任意の2点
が定義域で「凸である」とは,定義域内の任意の2点 ![]() に対して
に対して
![]() が連続なら内分点で
が連続なら内分点で
さらに2回微分可能なら定義域で二次導関数 ![]() の正負が一定である,
として同値である(ここではこれらの証明は略する).
の正負が一定である,
として同値である(ここではこれらの証明は略する).
ここでは,二次導関数の符号が一定である関数を凸関数と定め,なぜこのとき「凸関数」というのかを次の定理で理解したい.
関数 ![]() は定義域で2回微分可能で,
は定義域で2回微分可能で, ![]() の正負は一定である.このとき
定義域内の
の正負は一定である.このとき
定義域内の ![]() の
の
![]() 個の値
個の値
証明
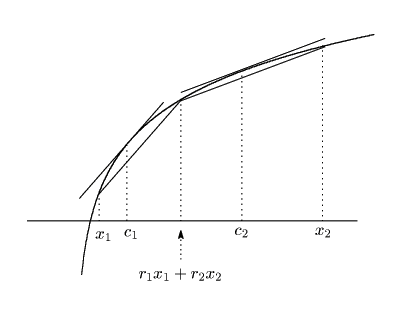
![]() として示す.
として示す.
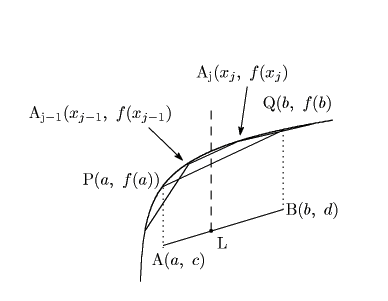 (1)から図のように辺
(1)から図のように辺
![]() と点
と点 ![]() は
直線
は
直線 ![]() に関して反対の側にある.したがって
に関して反対の側にある.したがって ![]() が
が
![]() 角形
角形 ![]() の外に出ることはない.
つまり線分
の外に出ることはない.
つまり線分
![]() となり
となり ![]() が凸多角形であることがわかる.□
が凸多角形であることがわかる.□
南海 すこしはわかっただろうか.論の組み立てはいろいろあるのだが, 数学的帰納法と平均値の定理を使ったところが,基本的なところだ.