


次: カタラン数
上: 相加相乗平均の不等式の証明
前: 特殊な函数を使うもの
関数の微分を使わずに数列だけで証明するには工夫がいる.
方法 7
次の命題を  とおく.
とおく.
このとき次の問いに答えよ,ただし  は
は  、および
、および の自然数とする.
の自然数とする.
 を示せ.
を示せ.
-
 を示せ.
を示せ.
 が成立すれば
が成立すれば
 が成立することを示せ.
が成立することを示せ.
 の自然数
の自然数 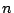 に対して
に対して  が成立することを示せ.
が成立することを示せ.
解
-

等号成立は  のとき.
ゆえに
のとき.
ゆえに  .
.
- まず
 を示す.
を示す.
したがって
 なので(1)と合わせて
帰納法により
なので(1)と合わせて
帰納法により
 である.
である.
 とする.つまり
とする.つまり
ここで
 を代入する.
を代入する.
つまり
 .
.
 の任意の自然数
の任意の自然数 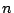 に対して
に対して
となる自然数 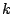 をとる.
をとる.
(2)より
 .
つぎに(3)の操作を
.
つぎに(3)の操作を  回繰り返し用いると
回繰り返し用いると
となり が成立することが示された.□
が成立することが示された.□
同様にたいへんうまい工夫がされている.これも入試問題になったことがある.
雜誌『初等数学』(2001年3月号)の宮地俊彦先生の報告によると,
1997年の『数学セミナー』(9月号)に掲載されたそうである.
方法 8
 に対して
に対して
を示せ.
-
を示せ.等号が成立する条件を
 の関係で述べよ.
の関係で述べよ.
-
を示せ.
-
を示し,等号成立が
 のときに限ることを示せ.
のときに限ることを示せ.
解
-
 のとき
のとき
ここで
 の符号と
の符号と
 の符号が
同じなので
の符号が
同じなので
等号成立は 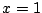 のときである.
のときである.
- (1)の
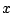 に
に
 を代入する.
を代入する.
これを整理して
を得る.等号が成立するのは
-
 を(2)の結果に代入することにより
を(2)の結果に代入することにより
となる.
- (3)から
 に対して
に対して

両辺
 にわたって加えることにより
にわたって加えることにより
を得る.  なのでこれから
なのでこれから
を得る.等号成立は
と帰納的に定まるので
 のときに限る.□
のときに限る.□
2は別解がある.
ただし定積分を使う.雜誌『初等数学』(2001年3月号)の宮地俊彦先生の報告による.
方法 9
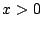 で定義された 関数
で定義された 関数  を
を
とする.

を正の数とし,定積分
を考えることにより,2を示せ.
解

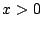 で定義された 関数
で定義された 関数  を
を
と定める.  は単調減少関数である.
は単調減少関数である.
ここで
である.
そこで
 のとき
のとき
 のとき
のとき
いずれの場合も2が(  の場合で)示されている.□
の場合で)示されている.□
これもよく知られたものだが,感心するほどうまく工夫されている.
方法 10
-
 である任意の正数
である任意の正数  に対し
に対し
を示せ.
-
 である任意の
である任意の 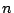 個の正数
個の正数
 に対し,
に対し,
を示せ.
-
を示し,等号成立が
 のときに限ることを示せ.
のときに限ることを示せ.
解
-
 である任意の正数
である任意の正数  に対し
に対し
等号成立は 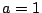 または
または  のとき.
のとき.
- 数学的帰納法で示す.
 のとき.
のとき.  より一方が1以上で,他方が1以下である.
ゆえに(1)より
より一方が1以上で,他方が1以下である.
ゆえに(1)より
なので成立している.
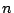 で成立するとし
で成立するとし  での成立を示す.
での成立を示す.
 である.ここで1以上のものと1以下のものを選ぶ.
番号を付け替えて
である.ここで1以上のものと1以下のものを選ぶ.
番号を付け替えて
 としてよい.
としてよい.
 とおくと
とおくと
 .帰納法の仮定から
.帰納法の仮定から
(1)から
なので
等号は
 かつ
かつ  のとき,
つまり
のとき,
つまり
 のときである.
のときである.
ゆえに  でも成立した.
でも成立した.
よって一般に
 である任意の
である任意の 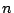 個の正数
個の正数
 に対し,
に対し,
が成立する.
-
とすると
ゆえに(2)から
つまり
である.
等号成立は(2)から
 ,つまり
,つまり
 のときに限る.□
のときに限る.□
なんとなんと,こんなこともできる.雜誌『初等数学』(2001年3月号)の宮地俊彦先生によると
(3)の不等式はWIGERTの不等式 というそうだ.
方法 11
各
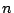
に対して

として一般性を失わない.
このとき
-
を示せ.
-
を示せ.
-
を示せ.
-
を示し,等号成立が
 のときに限ることを示せ.
のときに限ることを示せ.
解
-
 なので
なので
等号成立は  のときである.
のときである.
-
 ,
,
 なので
なので
である.
- (1)より
(2)とあわせて

つまり
- (3)より
等号成立は
のときに限る.つまり
 のときに限る.□
のときに限る.□



次: カタラン数
上: 相加相乗平均の不等式の証明
前: 特殊な函数を使うもの
Aozora Gakuen
![]() とおく.
とおく.

![]() は
は ![]() 、および
、および![]() の自然数とする.
の自然数とする.

 を代入する.
を代入する.

![]() .
つぎに(3)の操作を
.
つぎに(3)の操作を ![]() 回繰り返し用いると
回繰り返し用いると

 を代入する.
を代入する.


![]() で定義された 関数
で定義された 関数 ![]() を
を

![]() で定義された 関数
で定義された 関数 ![]() を
を

![]() のとき
のとき

![]() のとき
のとき

![]() の場合で)示されている.□
の場合で)示されている.□
![]() のとき.
のとき. ![]() より一方が1以上で,他方が1以下である.
ゆえに(1)より
より一方が1以上で,他方が1以下である.
ゆえに(1)より
![]() で成立するとし
で成立するとし ![]() での成立を示す.
での成立を示す.
![]() である.ここで1以上のものと1以下のものを選ぶ.
番号を付け替えて
である.ここで1以上のものと1以下のものを選ぶ.
番号を付け替えて
![]() としてよい.
としてよい.
![]() とおくと
とおくと
![]() .帰納法の仮定から
.帰納法の仮定から
![]() でも成立した.
でも成立した.
![]() である任意の
である任意の ![]() 個の正数
個の正数
![]() に対し,
に対し,


 ,
,
