


次: 関連入試問題
上: カタラン数
前: カタラン数
耕一 カタラン数にどんな意味があるのですか.
南海 三つの例を練習問題にしよう.
例 1.5.3
次の確率を求めよ.
解答
500円硬貨を持った人が来れば右へ, 1000円札を持った人が来れば上へそれぞれ1区画ずつ進むこ
とにすれば, おつりがいらないのは次のような場合に実現する.
したがって, この事象の数は A から B へ対角線を越えて上半分に入ることなく, B に
至る最短経路の総数に等しい. そして, 全事象の数は A から B へ至る最短経路の総数に
他ならないから, 求める確率は
□
例 1.5.4
次の個数を求めよ.

円周上に  個の点がある.これらの点を2点ずつ結んで内部で互いに交わらない
個の点がある.これらの点を2点ずつ結んで内部で互いに交わらない
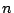 個の弦をひくとき,いく通りの違った方法があるか.
個の弦をひくとき,いく通りの違った方法があるか.
解答
求める方法の数を  とする. そして, 円周上の点を順に
とする. そして, 円周上の点を順に
 とおく. このとき, 2点を結ぶ弦を
とおく. このとき, 2点を結ぶ弦を
 のように表すことにし,
のように表すことにし,  を始点,
を始点,
 を終点とよぶことにする.
を終点とよぶことにする.
さて, 題意のような 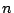 本の弦が引けた状態のうちの一つを考える. この状態におい
て,
本の弦が引けた状態のうちの一つを考える. この状態におい
て,
 を始点と終点に分け,
を始点と終点に分け,
とする. このとき, この始点と終点の組が題意をみたす(どの弦も互いに交わらない)ための
必要十分条件が
であることを, 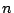 についての数学的帰納法で証明しよう.
についての数学的帰納法で証明しよう.
 のとき,
のとき,  が始点,
が始点,  が終点となるので,
明らかに成立する.
が終点となるので,
明らかに成立する.
 のときの成立を仮定し,
のときの成立を仮定し,  のときを考える.
のときを考える.
最初の設定より,  はつねに始点となる.
そこで,
はつねに始点となる.
そこで,  から順に見ていき, 最初に現れた終点を
から順に見ていき, 最初に現れた終点を
 とおく. すると, この点を終点とする弦が他の弦と交わらないの
であるから,
とおく. すると, この点を終点とする弦が他の弦と交わらないの
であるから,
 に対応する始点は
に対応する始点は
 の直前の
点, つまり
の直前の
点, つまり
 しかあり得ない.
しかあり得ない.
すると, 弦
 とこの2点を結
ぶ弧によってできる弓形(他の点を含まない方)の内部には他に弦がないから,
とこの2点を結
ぶ弧によってできる弓形(他の点を含まない方)の内部には他に弦がないから,  個の点から2個の点
個の点から2個の点
 を除いた残りの点について
は, それらを結ぶ弦が互いに交わらない. よって, 仮定よりこれら
を除いた残りの点について
は, それらを結ぶ弦が互いに交わらない. よって, 仮定よりこれら  個の点に
ついては
個の点に
ついては 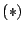 が成り立ち, これに
が成り立ち, これに
 を加え
ても, 始点, 終点がこの順に1個ずつ加えられるだけであるから,
を加え
ても, 始点, 終点がこの順に1個ずつ加えられるだけであるから,  のと
きも
のと
きも 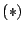 が成立する.
が成立する.
以上より, 求める方法の数は点
 から始
点, 終点を順に終点の前にある始点の個数が終点の個数よりも少なくないように選ぶ場合の
数, すなわち
から始
点, 終点を順に終点の前にある始点の個数が終点の個数よりも少なくないように選ぶ場合の
数, すなわち 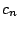 に他ならないから,
に他ならないから,
となる.□
注意
直接意味を考えて,
を示すこともできる. すると,
 は同一の漸化式をみたすので
は同一の漸化式をみたすので
となる.
例 1.5.5
凸 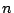 角形をその内部で交わらない対角線で三角形に分割するとき,
違った分割の仕方はいく通りあるか.
角形をその内部で交わらない対角線で三角形に分割するとき,
違った分割の仕方はいく通りあるか.
解答

条件を満たす分割の方法の総数を  とする.頂点を A1,A2,…An とおく.
とする.頂点を A1,A2,…An とおく.
 が対角線の一つであるような分割の仕方は,
が対角線の一つであるような分割の仕方は,
あるので, 結局,
ある. よって,  を通る対角線が関係するような分割の仕方は,
を通る対角線が関係するような分割の仕方は,
である. そして, これをすべての頂点について和をとると, 一つ一つの分割方法は, その分割
における対角線の数の2倍だけ繰り返し数えあげられることになる.
そこで, 一つの分割で用いられている対角線の本数を考えることにする.
いま, 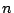 角形の内部に3角形は
角形の内部に3角形は  個できている. そして, 内部の対角線は二つずつの3角形に共有され, 辺は一つずつ用いられているので, 対角線の本数を
個できている. そして, 内部の対角線は二つずつの3角形に共有され, 辺は一つずつ用いられているので, 対角線の本数を  とすれば,
とすれば,
よって,
ただし,  である. すると,
である. すると,
であるから,
と予想することができる. そこで, これを数学的帰納法で証明する.
 のとき,
のとき,
より明らかに成立する.
-
 をみたすすべての
をみたすすべての 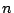 についての成立を仮定する. このとき,
についての成立を仮定する. このとき,
そして,
なので,
よって,
となるので,  のときも成立する.
のときも成立する.
したがって
となる.□



次: 関連入試問題
上: カタラン数
前: カタラン数
Aozora Gakuen
![]() 人の人がならんでいる.このうち
人の人がならんでいる.このうち ![]() 人が500円硬貨をもち,残りの
人が500円硬貨をもち,残りの
![]() 人は1000円札しかもっていない.切符は1枚500円である.切符を売りはじめるとき売場
にはお金がない.切符を買う人が誰も釣り銭ができるのを待たずにすむ確率はいくらか.
人は1000円札しかもっていない.切符は1枚500円である.切符を売りはじめるとき売場
にはお金がない.切符を買う人が誰も釣り銭ができるのを待たずにすむ確率はいくらか.![]() 人の人がならんでいる.このうち
人の人がならんでいる.このうち ![]() 人が500円硬貨をもち,残りの
人が500円硬貨をもち,残りの
![]() 人は1000円札しかもっていない.切符は1枚500円である.切符を売りはじめるとき売場
にはお金がない.切符を買う人が誰も釣り銭ができるのを待たずにすむ確率はいくらか.
人は1000円札しかもっていない.切符は1枚500円である.切符を売りはじめるとき売場
にはお金がない.切符を買う人が誰も釣り銭ができるのを待たずにすむ確率はいくらか.

![]() 個の点がある.これらの点を2点ずつ結んで内部で互いに交わらない
個の点がある.これらの点を2点ずつ結んで内部で互いに交わらない
![]() 個の弦をひくとき,いく通りの違った方法があるか.
個の弦をひくとき,いく通りの違った方法があるか.
![]() とする. そして, 円周上の点を順に
とする. そして, 円周上の点を順に
![]() とおく. このとき, 2点を結ぶ弦を
とおく. このとき, 2点を結ぶ弦を
![]() のように表すことにし,
のように表すことにし, ![]() を始点,
を始点,
![]() を終点とよぶことにする.
を終点とよぶことにする.
![]() 本の弦が引けた状態のうちの一つを考える. この状態におい
て,
本の弦が引けた状態のうちの一つを考える. この状態におい
て,
![]() を始点と終点に分け,
を始点と終点に分け,

![]() 角形をその内部で交わらない対角線で三角形に分割するとき,
違った分割の仕方はいく通りあるか.
角形をその内部で交わらない対角線で三角形に分割するとき,
違った分割の仕方はいく通りあるか.

![]() とする.頂点を A1,A2,…An とおく.
とする.頂点を A1,A2,…An とおく.
![]() が対角線の一つであるような分割の仕方は,
が対角線の一つであるような分割の仕方は,


