次： 素数が無数にあることの別証明 上： 素数の分布 前： 素数の分布

素数の分布とは

拓生　 素数を1から100までのなかで書くと

$$\begin{array}{l} 2,\ 3,\ 5,\ 7,\ 11,\ 13,\ 17,\ 19,\ 23,\ ... ... 53,\ 59,\ 61,\ 67,\ 71,\ 73,\ 79,\ 83,\ 89,\ 97 \end{array}$$

の25個あります．ところが5900から6000のなかでは

$$5903,\ 5923,\ 5927,\ 5939,\ 5953,\ 5981,\ 5987$$

の7個しかありません．

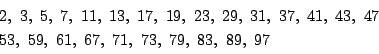
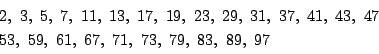
南海　　 5900から6000の間の素数はどのようにして見つけたのか．

拓生　 先の100までの素数のなかで

$$73^2=5329,\ 79^2=6241$$

ですから，73までの素数で順に割って割り切れるものを除いていきました．

5900から6000の間の数$N$が$N=mn$と因数分解できて$m\le n$とすると，$N=mn\ge m^2$となるので， 小さい方の素因数は73以下です．

南海　　 このように，小さい素数で割り切れるものを除いていくことで，新たな素数を発見していく方法が エラトステネスの篩(ふるい)といわれるものだ． 正整数$n$が素数であるかどうかを判定したければ，$p^2 \le n$の範囲の素数$p$で割ってみればよい． いずれでも割り切れなければ素数と判定してよい．

例えば1999は素数か．

拓生　 $43^2=1849$で$47^2=2209$ですから，2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 で割れるかどうかを調べればいいです． いずれでも割り切れないので素数です．

南海　　 このように，順に素数で割って割り切れる数をふるいにかけて除く．$N$までの数に対して $\sqrt{N}$以下の素数まで調べる． そのいずれでも割りきれずに残ったものが$N$以下の素数である．

エラトステネス（Eratosthenes，紀元前276頃〜前192頃)は古代ギリシアの数学者，天文学者，地理学者だった． 素数の選別法として有名な「エラトステネスの篩(ふるい)」を発見した． また、はじめて赤道の周囲を測量し、約45000 km と算出した人でもある．主著は「地理学」である．

何ともすごい人だ．日本列島はようやく弥生時代に入ったばかりの頃だ．

ところで「篩(ふるい)」を知っているか．

拓生　 「候補をふるいにかける」とか，「一次試験でふるい落とされる」などの言い方は知っていますが， 「篩(ふるい)」を見たことはありません．

南海　　 1831年(天保2)に薩摩藩主島津重豪(しまづしげひで)が曾槃・白尾国柱らに命じて作らせた農業書『成形図説』 に図が載っているので紹介しよう．この書は農事・五穀・疎菜・薬草・草木・鳥類などについて，和漢洋の諸書で 考証し，さらに綿密な図を掲げ，編纂させた百科全書である．全100巻の大部なものだ．和語，漢語，オランダ語の 名前を記し，説明を付けている．

拓生　 周りが鉄で出来ていて電気で振動するものを見たことがあります． 工事しているところで小石を除くのに使われています．

南海　　 そう．あれが篩だ．

少し回り道をしたが，さて君の質問は？

拓生　 1から100には24個もあるのに，5900から6000では7個しかありません．大きな数になるといろんな素数が それまでにあるので，だんだん新しい素数の出現が少なくなっていくのは，そうだろうと思うのですが． では，どのような割合で出現するのかとか，そういうことを聞きたいのです．

南海　　 なるほど．どのように素数が分布しているのかということを，素数の分布に関する問題という． これを考えるために，正の実数$x$を越えない素数の個数を$\pi(x)$と表そう．

拓生　

$$\pi(100)=24,\ \pi(6000)-\pi(5900)=7$$

ということですね．