一次変換を見る

2005.9.11

一次変換は平面全体の変換だ

南海　 今日は一次変換を目で見てみよう．
一次変換は平面全体を平面に移す変換だ． 個別の点や図形の行き先を見るだけではわかりにくい． そのために，平面上の各点について， それが一次変換でどの点に移るのかを図示するのだ．

拓生　 図示といっても，平面の点は無数にあります．

南海　 もちろんそうだ． それで格子点，つまり座標が整数である点について， その点と行き先とを線分で結んでいくのだ． $ A= \left( \begin{array}{cc} a&b\\ c&d \end{array} \right) $ とすれば， 格子点 $ (x,\ y) $ と $ (ax+by,\ cx+dy) $ を結んでいくのだ． これは点 $ (x,\ y) $ が点 $ (ax+by,\ cx+dy) $ に移るとも考えられるし， ベクトル $ (x,\ y) $ がベクトル $ (ax+by,\ cx+dy) $ に移るとも考えられる．

拓生　 それでもたくさんあります．計算はたいへんです．

南海　 そこで，プログラムだ．これはBASICの一番簡単な応用だ． ここでは文教大学の白石和夫先生が作られた十進BASICを使った．フリーソフトなので，手元のパソコンですぐに利用できる． プログラムは

SET WINDOW -10,10,-10,10
INPUT PROMPT "a,b,c,d=":a,b,c,d
FOR M=-10 TO 10 STEP 1
FOR N=-10 TO 10 STEP 1
SET AREA COLOR 4
DRAW disk WITH SCALE(0.05)*SHIFT(M,N)
DRAW circle WITH SCALE(0.15)*SHIFT(a*M+b*N,c*M+d*N)
PLOT LINES: M ,N ; a*M+b*N,c*M+d*N
NEXT N
NEXT M
END

固有方程式が2実解の場合

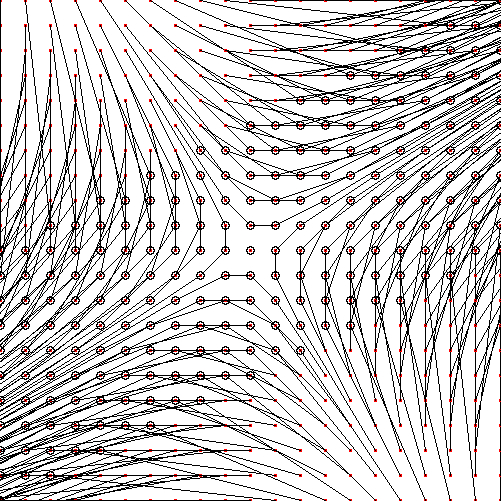
拓生　 早速， $ a=2,\ b=1,\ c=1,\ d=1 $ を代入してみました．

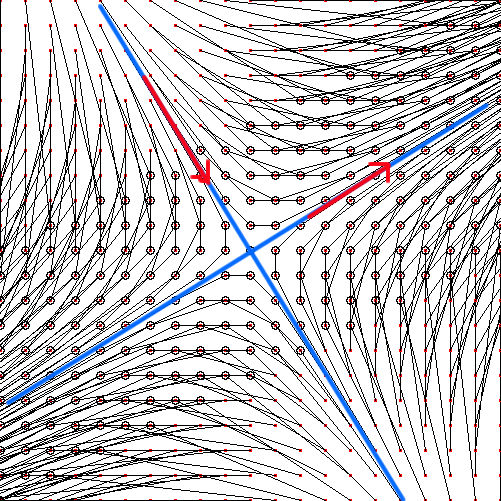
南海　 この方向はどのようにして求めるのだったか．

拓生　 それが固有値と固有ベクトルです． 行列 $ A $ を $ A= \left( \begin{array}{cc} a&b\\ c&d \end{array} \right) $ とする． \[ A\overrightarrow{u}=t\overrightarrow{u} \] となるベクトルが固有ベクトルです． つまり \[ \left( \begin{array}{cc} a-t&b\\ c&d-t \end{array} \right) \] です， このようなベクトル $ \overrightarrow{u} $ で 零ベクトルでないものが存在するためには 左辺の行列 $ \Delta $ が0，つまり \[ (a-t)(d-t)-bc=0 \] です．これを整理すると \[ t^2-(a+d)t+ad-bc=0 \]

南海　 これを固有方程式という．

拓生　 今の場合 \[ t^2-3t+1=0 \] これを解いて \[ t=\dfrac{3\pm\sqrt{5}}{2} \] です． \[ \left( \begin{array}{cc} a-t&b\\ c&d-t \end{array} \right) = \left( \begin{array}{cc} \frac{1\mp\sqrt{5}}{2}&1\\ 1&\frac{-1\mp\sqrt{5}}{2} \end{array} \right) \] ですから固有ベクトルとして例えば \[ \overrightarrow{u}= \left( \begin{array}{c} 1\mp\sqrt{5}\\ 2 \end{array} \right) \] がとれます．実際 \[ \left( \begin{array}{cc} 2&1\\ 1&1 \end{array} \right) \left( \begin{array}{c} 1\mp\sqrt{5}\\ 2 \end{array} \right) =\dfrac{3\pm\sqrt{5}}{2} \left( \begin{array}{c} 1\mp\sqrt{5}\\ 2 \end{array} \right) \] この方向が2本直線の方向なのですね．

南海　 今は方程式 \[ t^2-(a+d)t+ad-bc=0 \] が異なる2実解をもった． これが他の場合にどのようになるかを見ていこう．

重解の場合

南海　 \[ A= \left( \begin{array}{cc} 3&-1\\ 1&1 \end{array} \right) \] ではどうか．

拓生　 このとき固有方程式は \[ t^2-4t+4=0 \] で重解です．やってみます．

南海　 それはまた，『線型代数入門』に書く予定だ．それを見てほしい． 今は例を作ってみよう．

虚数解の場合

南海　 \[ A= \left( \begin{array}{cc} 1&2\\ -1&2 \end{array} \right) \] ではどうか．

拓生　 このとき固有方程式は \[ t^2-3t+4=0 \] で虚数解です．やってみます．

南海　 虚数解の場合は固定された方向は( $ xy $ 平面上には)存在しない．

回転の場合

南海　 \[ A \left( \begin{array}{cc} \cos 60^{\circ}&-\sin 60^{\circ}\\ \sin 60^{\circ}&\cos 60^{\circ} \end{array} \right) \] の近似として \[ \left( \begin{array}{cc} 0.5&-0.87\\ 0.87&0.5 \end{array} \right) \] ではどうか．

拓生　 やってみます．

その他の場合
その1

南海　 \[ A= \left( \begin{array}{cc} 2&1\\ 3&4 \end{array} \right) \] ではどうか．

拓生　 このとき固有方程式は \[ t^2-6t+5=0 \] で，解は $ 1,\ 5 $ です．やってみます．

南海　 これは一つの固有ベクトルが動かない場合だ． このように1次変換は見ることができる． プログラムを工夫して，遊んでみてほしい．

その2

拓生　 \[ A= \left( \begin{array}{cc} 2&1\\ 4&-1 \end{array} \right) \] でやってみました． このとき固有方程式は \[ t^2+t-6=0 \] で，解は $ -3,\ 2 $ と，最初の場合と異なり，固有値が正と負です．

その3

拓生　 \[ A= \left( \begin{array}{cc} -4&1\\ -2&-1 \end{array} \right) \] でやってみました． このとき固有方程式は \[ t^2+5t+6=0 \] で，解は $ -3,\ -2 $ と，固有値がともに負です．