太郎
南海 そこで,この問題を次のように一般化した.
南海
数列![]() はシルベスター数列といわれる.
Sylvester's sequenceには大きい値の因数分解も載っている.
はシルベスター数列といわれる.
Sylvester's sequenceには大きい値の因数分解も載っている.
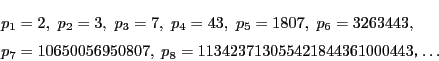
太郎 一気に大きくなるのですね.
南海 そこで,自然数の逆数和で1を超えないものの最大値が, このシルベスターの数列によって与えられると考え, 定理1にまとめたのだ.
この定理はさらに一般化される.最後にそれを証明する.
証明
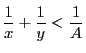 のとき
のとき
![]() なので自然数
なので自然数![]() をとって
をとって![]() とおく.
とおく.
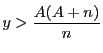 ,つまり
,つまり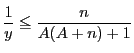 .
よって
.
よって
ここで
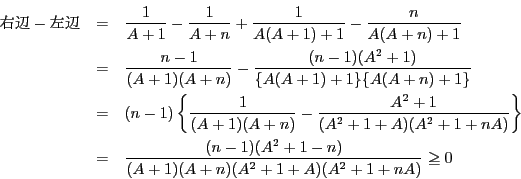
![]() のときは,
のときは,![]() で,
で,![]() も必要なので
も必要なので![]() .
よってこのときも,不等式(1)は成立する.
したがって,条件を満たすすべての
.
よってこのときも,不等式(1)は成立する.
したがって,条件を満たすすべての![]() と
と![]() に関して
に関して
よって本命題が示された. □
これを用いれば,変数の個数が決まっているときは,条件を絞りながら,個別に調べることで,最大値を与える数列を決定することができる. 実際,この命題1と同じ命題,およびその3変数への拡張を用いて,栃木県の先生が,4変数,5変数の場合について考察しておらる.数研通信66号(2010年1月)所収の論文である.
しかし,一般の自然数でつねに定理1が成立することの証明は, 次元が異なる問題になる.
太郎 個別に確認する方法があるということと, 一般的に証明することができるということは,異なることなのですね.
南海 そうなのだ.当初,この命題を用いれば定理1が証明できると考え次のところまで書いた.しかしこの方向ではできなかった.
途中で止まった証明
![]() の項の中に
の項の中に![]() と一致しないものがあるとする.
それを小さい方から見て最初に
と一致しないものがあるとする.
それを小さい方から見て最初に![]() と異なるものを
と異なるものを![]() とする.
とする.
![]() と仮定する.
と仮定する.![]() なので
なので
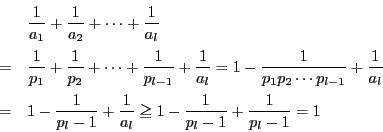
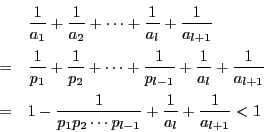
である.
ここで命題1を
![]() で用いる.
で用いる.
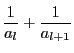 が最大となるのは
が最大となるのは
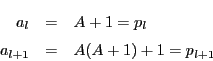
しかし,これから
太郎
確かに.個別の![]() のときには,その他の場合をすべて調べて,消してゆけばよいですが,しかしそれで一般の場合を示せるかというと,簡単ではないのですね.
のときには,その他の場合をすべて調べて,消してゆけばよいですが,しかしそれで一般の場合を示せるかというと,簡単ではないのですね.
南海
困っているときに,教え子で数学科に進んだせきさんから,
定理1を証明している論文「
APPROXIMATING 1 FROM BELOW USING n EGYPTIAN FRACTIONS(![]() 個のエジプト分数による1の下からの近似)
」(K.SOUNDRARAJAN) を紹介された.ここには一つすばらしい着想がある.
個のエジプト分数による1の下からの近似)
」(K.SOUNDRARAJAN) を紹介された.ここには一つすばらしい着想がある.
上記論文の証明は,ムーアヘッドの不等式を用いる.この不等式は,数学セミナー2009年2月号,「特集:不等式の世界」で岡山理科大の示野信一先生が「対称式と不等式」と題してムーアヘッドの不等式について書いておられた.それを参考にした.後にまた『不等式』(G.H.ハーディ/J.E.リトルウッド著,細川尋史訳,シュプリンガー社)も手に入れた.ここには詳しく述べられている.ムーアヘッドの不等式はそれ自身たいへんおもしろい不等式である.
この不等式を用いれば,定理1と命題1を統合し,より一般的な形で証明することができる.
そこで,上記論文などを参考にして,高校範囲で証明するために,それぞれ独自に論証を再編した.責任は南海にある.