


次: 生成関数
上: 生成関数の方法
前: 生成関数の方法
耕一
2000年の横浜国立大学の入試問題の別解を見ました.
南海
生成関数で解くというものだな.
耕一
はい.
それとよく似た問題が98年北海道大学にあります.
南海
よくしっているな.それぞれを紹介しよう.
例 1.3.1
[00横浜国立大学]
数列  を
を
で定める.次の問いに答えよ.
 を求めよ.
を求めよ.
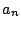 を求めよ.
を求めよ.
例 1.3.2
[98北大後期理系]
次の条件で定まる 数列  の一般項を求めよ.
の一般項を求めよ.
南海 普通は推測して帰納法で解く.
横国大の解答は問題のところにあるがここに再掲載しておこう..
北大の普通の解答は耕一君に作ってもらおう.
耕一 はい.
解答[00横浜国立大学]
-
-
 と推測される.
これを数学的帰納法で示す.
と推測される.
これを数学的帰納法で示す.
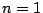 のとき,
のとき,  より成立.
より成立.
-
 で成立するとする.
このとき
で成立するとする.
このとき
よって  でも成立する.
でも成立する.
- 以上から
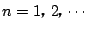 に対し
に対し
 が示された.□
が示された.□
解答[98北大]
これから
と推測される.数学的帰納法で示す.
 では成立した.
では成立した.
 のとき成立するとして,
のとき成立するとして,
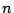 のときに成り立つことを示せばよい.
条件式は等式であるから,結局条件式の右辺に
のときに成り立つことを示せばよい.
条件式は等式であるから,結局条件式の右辺に
 のときの
のときの 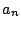 を代入
して計算した結果,条件式の左辺になればよい.
を代入
して計算した結果,条件式の左辺になればよい.
ゆえに 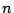 のときも成立し,
のときも成立し,
が示せた.□
Aozora Gakuen
![]() を
を

 を求めよ.
を求めよ.
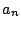 を求めよ.
を求めよ.



