


次: ある入試問題の一般化への生成関数の活用
上: 生成関数の方法
前: 生成関数による別解
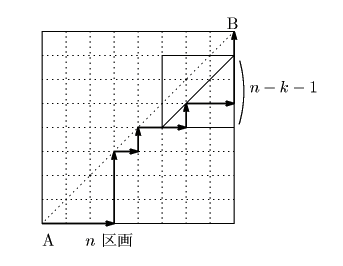 図1のように
図1のように 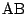 が対角線である正方形の各辺が
が対角線である正方形の各辺が 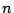 に区切られ,小正方形
に区切られ,小正方形 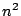 に分け
られている.
に分け
られている.
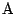 から
から 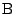 への最短経路のうち対角線
への最短経路のうち対角線 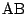 より上半分には出ない
(対角線に乗るところまでは許される)経路の総数を
より上半分には出ない
(対角線に乗るところまでは許される)経路の総数を 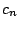 とする.ただし
とする.ただし 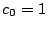 とする.
とする.
経路が最後に対角線に乗った番号で分類することにより,
なぜなら
すべての経路を, 最後に対角線に乗った番号で分類する. 対角線 AB 上第 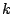 番
番
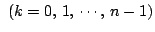 までの経路の総数は
までの経路の総数は
このあとは再び対角線には乗らないのであるから, 図のように
したがって,
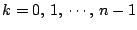 の各場合の数を加えることにより
の各場合の数を加えることにより
とする.すると
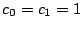 であることに注意すると,
であることに注意すると,
を得る.
ここで 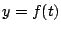 とおこう.
とおこう.
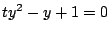 より,
より,
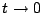 のとき
のとき 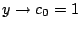 とならねばならないので,
とならねばならないので,
ここで, 一般に何度も微分できる関数 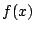 は
は
と級数に展開されることを用いる.これは 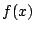 を
を
とおくと
より
となるのでわかる.
この 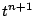 の係数は
の係数は
よって,
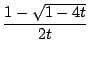 の
の 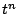 の係数は
の係数は
つまり,
耕一 なるほど.
南海 入試問題もその気になって探求すると,いろんな広がりがあるのだ.



次: ある入試問題の一般化への生成関数の活用
上: 生成関数の方法
前: 生成関数による別解
Aozora Gakuen
 図1のように
図1のように ![]() 番
番
![]() までの経路の総数は
までの経路の総数は
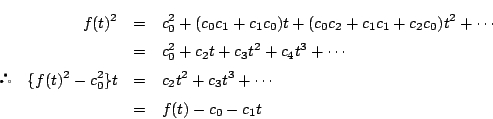
![]() とおこう.
とおこう.
![]() より,
より,
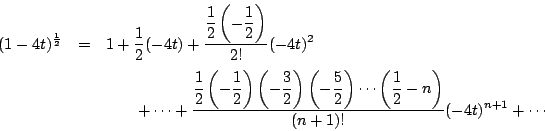
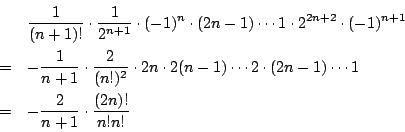
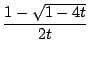 の
の