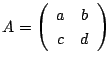一次変換から線型写像へ

次: ベクトル空間と線型写像の定義上: ベクトル空間と線型写像前: ベクトル空間と線型写像

一次変換から線型写像へ

南海　 2005年辺りから，高校数学に一次変換が復活している．これはいいことだ．だが今回の課程変更で導入された一次変換は，行列による座標平面の個別の点の移動という観点だけである．これでは，一次変換の意義がよくわからない． 10年以上前の課程では，次の2つの観点がはっきりしていた．

平面全体の変換であること．
ベクトルの集合からベクトルの集合への写像である．

これが2005年からの教科書ではあいまいである．

（2012年9月追記：2005年の一次変換復活を述べて7年，2012年に1年の学年あたりから再び行列と一次変換がなくなる．愚かなことである．高校時代に学ぶべきことが，この10年で変化したというのか．まったくそのようなことはない．やはり最低限，2次行列の扱いと平面ベクトルの一次変換の考え方を知っておくことは必要である．

この対話は，高校でそれを習うことを前提にしている．高校範囲の部分を書いておく余裕がない．意欲的な高校生はぜひ行列や一次変換の入った教科書や参考書を図書館などで見つけ，基本事項を読んでほしい．数時間から数日で可能である．高校時代にいちど触れておくなら，大学での線型数学の理解がそれだけ容易になる．）

南海　また大学生になって最初にとまどうのが「線型代数」だ．『線型代数』や『行列と行列式』と題した参考書はたくさんある．しかし，計算処理の方法が中心である参考書と，線型空間の一般的な定義からはじめる教科書風のものとに分かれていて，線型代数の基礎概念を高校数学の内容の分析からはじめて，概念を掘りさげていく参考書は少ないように思われる．

それは，大学生向けの書物が，高校数学を数学とは見なさず単なる受験数学と見なし，大学生の数学を高校数学とは切り離されたところからはじめるからである．青空学園数学科は，高校数学を数学という学問として考え，学んでいこうという立場である．この立場からすると，高校数学を掘りさげることで線型代数の基礎概念を学ぶことが大切であり，またそれは可能である．

そこで大学初年度の線型代数とつながるように，線型代数の考え方を話していこう．高校数学では2次，つまり平面までなのだが，ここでは基礎概念の意味を考えながら，できるだけ一般的に定義し，計算は可能なかぎり3次行列も材料にすることにしよう．また，例や演習のなかでは，数学Cで習ったことは既知とする．まず，一次変換とは何か．

耕一　一次変換とは，行列 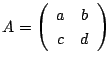$A=\matrix{a}{b}{c}{d}$ によって，平面の点 $(x,\ y)$ を，次の式で定まる点 $(X,\ Y)$ に移す変換のことです．

$\begin{displaymath} \vecarray{X}{Y}=\matrix{a}{b}{c}{d}\vecarray{x}{y} \end{displaymath}$

つまり点 $(x,\ y)$ を点 $(X,\ Y)=(ax+by,\ cx+dy)$ に移す変換のことです．

これは空間の場合も同様です．空間の場合，一次変換とは行列 $A=\left( \begin{array}{ccc} a&b&c\\ d&e&f\\ g&h&i \end{array}\right)$ によって，空間の点 $(x,\ y,\ z)$ を次の式で定まる点 $(X,\ Y,\ Z)$ に移す変換のことです．

$\begin{displaymath} \left( \begin{array}{c} X\\ Y\\ Z \end{array}\right) = ... ...ght) \left( \begin{array}{c} x\\ y\\ z \end{array}\right) \end{displaymath}$

つまり点 $(x,\ y,\ z)$ を点 $(X,\ Y,\ Z)=(ax+by+cz,\ dx+ey+fz,\ gx+hy+iz)$ に移す変換のことです．

南海　それで正しい．変換とは集合から同じ集合への写像のことをいう．いまの場合は平面という点の集合から平面への写像になっている．一次というのは，式が(定数項のない)一次式になっているからだ．

一次変換の全体像を見るために，平面上の点がどのように移動されるかを見てみよう．簡単なプログラムを組めばよい．ここでは文教大学の白石和夫先生が作られた十進BASICを使う． http://www.vector.co.jp/authors/VA008683/ にあるフリーソフトなので，手元のパソコンですぐに利用できる．プログラムは

SET WINDOW -10,10,-10,10
INPUT PROMPT "a,b,c,d=":a,b,c,d
FOR M=-10 TO 10 STEP 1
   FOR N=-10 TO 10 STEP 1
      SET AREA COLOR 4
      DRAW disk WITH SCALE(0.05)*SHIFT(M,N) 
      DRAW circle WITH SCALE(0.15)*SHIFT(a*M+b*N,c*M+d*N) 
      PLOT LINES: M ,N ; a*M+b*N,c*M+d*N
   NEXT N
NEXT M
END

である．これは，始点を赤の点「・」で，終点を小円「○」にとり，それを線分で結んだものが得られる．『一次変換を見る』にいろんな例を作ってみた．参考にしてほしい．

行列を

$\begin{displaymath} A=\matrix{1}{3}{2}{2} \end{displaymath}$

とする．このときは次のようになる．

耕一　確かによくわかります．今は2次元，3次元で考えましたが， 1次元の場合に考えると，数直線上の点をに移す変換ではありませんか．これって正比例関数です．

南海　一次変換は1次元の場合は正比例関数そのものだ．それを高次元に一般化したものだ．いま「正比例関数」といったように，これは関数だ．つまり，一次変換は単なる点の変換以上の意味，関数，あるいは写像なのだ．一次変換は点の変換であるが，同時にまたベクトル $\overrightarrow{u}=(x,\ y)$ をベクトル $\overrightarrow{v}=(X,\ Y)=(ax+by,\ cx+dy)$ に移す写像とも考えられる．

耕一　ベクトルからベクトルへの写像ですか．写像というのは，集合から集合への関数のようなものでした．すると，ベクトルの集合を考えるのですか．

南海　その通りだ．ベクトルの集合がベクトル空間になるのだ．先ほどの例を，ベクトルでいえば図のように，赤ベクトルが青ベクトルに変換されるのだ．

さて，一次変換をベクトルの写像と見るとき，どのような性質があるかを考えたい．そこでまずベクトルにはどんな演算があったか．

耕一　加法，減法と実数倍です．さらに，実数とベクトル $\overrightarrow{u},\ \overrightarrow{v}$ に対して

$\begin{displaymath} k(\overrightarrow{u}+\overrightarrow{v})=k\overrightarrow{u}+k\overrightarrow{v} \end{displaymath}$

が成り立ちます．いわゆる分配法則です．

南海　もう少し一般的に演算法則は書いた方がいいが，とにかくいわゆる分配法則が成り立つように，実数倍が定義されている．このような演算が定まっているベクトルの集合をベクトル空間という．次に，「式が(定数項のない)一次式」なので一次変換というわけだが，定数項がないことは，写像としては何を意味するのか．

耕一　点の変換という見方でいえば xy 平面の原点が，原点に移ります．つまり一次変換は原点を動かしません．しかしそれ以上のことはわかりません．

南海　一次変換をベクトルの写像として考えよう．つまりベクトル $\overrightarrow{u}=(x,\ y)$ を，

$\begin{displaymath} \overrightarrow{v}=\matrix{a}{b}{c}{d}\overrightarrow{u} \end{displaymath}$

によって，ベクトル $\overrightarrow{v}$ にうつす．これをさらに

$\begin{displaymath} \overrightarrow{v}=f(\overrightarrow{u}) \end{displaymath}$

と書こう．

はベクトル空間からベクトル空間への写像になる．ベクトルの演算である和と実数倍と，この写像の関係は？

耕一　

$\begin{eqnarray*} f(k\overrightarrow{u})&=&\matrix{a}{b}{c}{d}k\overrightarrow{u... ...rightarrow{v})\\ &=&f(\overrightarrow{u})+f(\overrightarrow{v}) \end{eqnarray*}$

です．

Aozora Gakuen