


次: 行列の対角化
上: 固有ベクトルと線型写像の対角表現
前: 固有ベクトルと線型写像の対角表現
南海
線型写像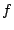 に対して,一組の基底
に対して,一組の基底
をとると,線型写像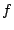 には,その基底の像をもとの基底で表したとき
には,その基底の像をもとの基底で表したとき
となる行列
が対応するのだった.
そこで基底をうまくとって,
この行列が対角行列になるようにできないか,という問題が起こる.
ただし,対角行列とは,
となる行列のことをいう.
耕一
それは
つまり
となる1次独立な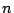 個のベクトルが見つかればいいということですね.
個のベクトルが見つかればいいということですね.
南海
そこで,線型写像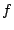 に対して
に対して
 |
(1.3) |
となるベクトル
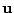 を,
固有値
を,
固有値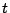 に対する固有ベクトルという.
固有値と固有ベクトルを具体的に計算するために,
一組の基底が固定され,線型写像が上のように行列で表されているとする.
に対する固有ベクトルという.
固有値と固有ベクトルを具体的に計算するために,
一組の基底が固定され,線型写像が上のように行列で表されているとする.
耕一
すると関係式(1.3)は
となります.
南海
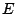 を単行列とすれば
を単行列とすれば
である.零ベクトルでない解
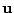 が存在するためには,行列式
が存在するためには,行列式
が必要十分な条件である.
この行列式は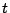 の
の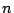 次多項式である.
これを固有多項式という.
次多項式である.
これを固有多項式という.
耕一
 のとき.
のとき.
 のときは複雑になります.
のときは複雑になります.
南海
うまく行列や小行列でまとめた.
耕一
線型写像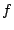 に対して一組の基底をとり,行列
に対して一組の基底をとり,行列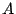 を定め,
それによって固有多項式ができました.
基底のとり方をかえれば多項式は変わるのですか.
を定め,
それによって固有多項式ができました.
基底のとり方をかえれば多項式は変わるのですか.
南海
基底のとり方をかえれば,対応する行列は
に変わる.このとき
なので,固有多項式は変わらない.つまり固有多項式は線型写像によって定まる.
それでこれ以降,固有多項式を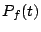 のように表すことにする.
すると既に見たように,
のように表すことにする.
すると既に見たように,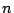 次方程式
次方程式
の根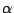 に対して
に対して
となるベクトル
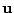 が存在する.
が存在する.
これが固有値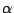 に対応する固有ベクトルである.
に対応する固有ベクトルである.
定理 5
線型写像
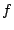
の固有多項式を
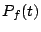
とする.
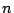
次方程式
に異なる0でない根

があるとき,それらの根に対応する固有ベクトル
は一次独立である.
証明
 についての数学的帰納法で示す.
についての数学的帰納法で示す.
 のとき.
のとき.
 が一次従属なら
が一次従属なら
となる0でない数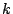 がある.ところが
がある.ところが
となり,ベクトル
 の固有値が
の固有値が となる.
これは
となる.
これは
 に反する.
に反する.
 のとき成立するとし,
のとき成立するとし, のときも成立することを示す.
ここで,
のときも成立することを示す.
ここで,
は一次従属であるとする.
するとベクトル
 は,
すべては0ではない係数
は,
すべては0ではない係数
 を用いて
を用いて
と他の 個のベクトルで表される.
個のベクトルで表される.
より
これから
数学的帰納法の仮定から
は一次独立である.
したがって
 のうちには0でないものが存在するので,
のうちには0でないものが存在するので,
 がすべて異なることとに反する.
ゆえに
がすべて異なることとに反する.
ゆえに
は一次独立である.
 で成立したので,定理が示された.□
で成立したので,定理が示された.□



次: 行列の対角化
上: 固有ベクトルと線型写像の対角表現
前: 固有ベクトルと線型写像の対角表現
Aozora Gakuen
![]() に対して,一組の基底
に対して,一組の基底



![]() に対して
に対して
![]() を単行列とすれば
を単行列とすれば

![]() のとき.
のとき.

![]() のときは複雑になります.
のときは複雑になります.

![]() に対して一組の基底をとり,行列
に対して一組の基底をとり,行列![]() を定め,
それによって固有多項式ができました.
基底のとり方をかえれば多項式は変わるのですか.
を定め,
それによって固有多項式ができました.
基底のとり方をかえれば多項式は変わるのですか.

![]() に対応する固有ベクトルである.
に対応する固有ベクトルである.
![]() についての数学的帰納法で示す.
についての数学的帰納法で示す.
![]() のとき.
のとき.
![]() が一次従属なら
が一次従属なら

![]() のとき成立するとし,
のとき成立するとし,![]() のときも成立することを示す.
ここで,
のときも成立することを示す.
ここで,



