


次: 内積の対角型行列表示
上: 内積と直交変換
前: 内積と直交変換
南海
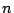 次元ベクトル空間
次元ベクトル空間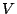 の内積をもう一度考えよう.
の内積をもう一度考えよう.
いま一組の基底
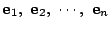 をとる.
内積は1節ですでに定義している.
ベクトル空間
をとる.
内積は1節ですでに定義している.
ベクトル空間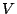 の2つのベクトル
の2つのベクトル
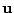 と
と
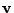 に対して内積
に対して内積
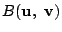 といわれる実数値が定まる,
その定義は内積の定義(4)を見てほしい.
一言でいえば,2つのベクトルを変数とし,
双線型で正の値をとる対称実数値関数ということである.
といわれる実数値が定まる,
その定義は内積の定義(4)を見てほしい.
一言でいえば,2つのベクトルを変数とし,
双線型で正の値をとる対称実数値関数ということである.
とする.このとき
と基底によって定まる一定の行列を用いて表される.
耕一
なので,この行列は左上から右下への対角線に関して対称です.
南海
このような行列を対称行列と呼ぼう.
またベクトル
を
のように成分で書いて1行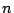 列の行列と同一視しよう.そして縦に書いたベクトルは
列の行列と同一視しよう.そして縦に書いたベクトルは
のように表す.
一般に記号 は行列
は行列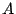 の
の 行
行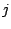 列の成分を
列の成分を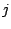 行
行 列の成分と入れ替えた行列を表す.
列の成分と入れ替えた行列を表す.
 を行列
を行列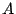 の転置行列という.
すると内積は対称行列
の転置行列という.
すると内積は対称行列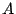 を用いて
を用いて
と書くことができる.ただし
である.
耕一
逆に対称行列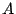 を用いて
を用いて
で
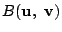 を定義すると,これは内積になりますか.
あっ,正の値をつねにとるかどうかがわからないのですね.
を定義すると,これは内積になりますか.
あっ,正の値をつねにとるかどうかがわからないのですね.
南海
双線型な実数値関数が得られるが,正値かどうかは未定である.
一般に,基底を一つ固定したとき対称行列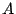 に対して定まる
に対して定まる
を双線型形式と呼ぼう.
また対称行列に対して定まる
を二次形式と呼ぼう.
二次形式があれば次のようにして双線型形式が定まる.
これが双線型形式であることを確認してほしい.
耕一
ですが,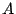 が対称行列なので
が対称行列なので
です.ゆえに
となります.
南海
とし,
 とすれば,二次形式とはどのようなものになるか.
とすれば,二次形式とはどのようなものになるか.
耕一
です.
ここで とすると,
『数学対話』−「パスカルの定理」−「特別な場合の演習問題」に出てきた2次曲線の一般形です.
とすると,
『数学対話』−「パスカルの定理」−「特別な場合の演習問題」に出てきた2次曲線の一般形です.
Aozora Gakuen
![]() をとる.
内積は1節ですでに定義している.
ベクトル空間
をとる.
内積は1節ですでに定義している.
ベクトル空間![]() の2つのベクトル
の2つのベクトル
![]() と
と
![]() に対して内積
に対して内積
![]() といわれる実数値が定まる,
その定義は内積の定義(4)を見てほしい.
一言でいえば,2つのベクトルを変数とし,
双線型で正の値をとる対称実数値関数ということである.
といわれる実数値が定まる,
その定義は内積の定義(4)を見てほしい.
一言でいえば,2つのベクトルを変数とし,
双線型で正の値をとる対称実数値関数ということである.



![]() を用いて
を用いて
![]() に対して定まる
に対して定まる


