

 次: 数学的帰納法か直接証明か
上: 整式と見るか整数と見るか
前: 整式の決定[00お茶の水大]
次: 数学的帰納法か直接証明か
上: 整式と見るか整数と見るか
前: 整式の決定[00お茶の水大]
問題
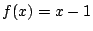 ,
,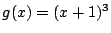 であるとき
であるとき
をみたす整式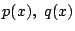 の組のなかで,
の組のなかで,
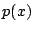 の次数が最小である組,
および,
の次数が最小である組,
および,
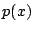 の最高次数の項の係数が1であるなかで,次数が最小の組をそれぞれ求めよ.
の最高次数の項の係数が1であるなかで,次数が最小の組をそれぞれ求めよ.
解1
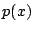 は
は
つまり,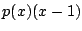 を
を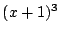 で割った余りが1ということで特徴づけられる.
ここで
で割った余りが1ということで特徴づけられる.
ここで
なので
従って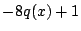 が
が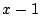 で割りきれなければならない.
で割りきれなければならない.
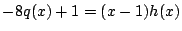 とおく.これを
とおく.これを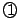 に代入し
に代入し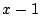 で約する.
で約する.
このとき作り方から
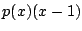 を
を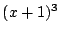 で割ると1余る.
つまり,
で割ると1余る.
つまり,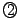 の形に書けることが
の形に書けることが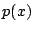 の満たすべき必要十分条件である.
の満たすべき必要十分条件である.
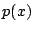 の次数が最小であるのは
の次数が最小であるのは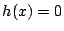 のときで
のときで
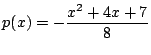 .
このとき
.
このとき
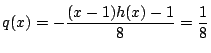 .
.
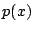 の最高次数の項の係数が1であるなかで,次数が最小であるのは,
の最高次数の項の係数が1であるなかで,次数が最小であるのは,
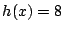 のときで
のときで
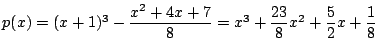 .
このとき
.
このとき
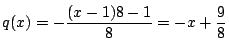 である.
である.
解2
である.
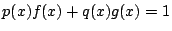 から辺々引いて
から辺々引いて
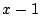 と
と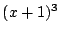 は互いに素なので
は互いに素なので
と,ある整式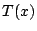 を用いて書け,この形をしていれば条件を満たす.
よって条件を満たす
を用いて書け,この形をしていれば条件を満たす.
よって条件を満たす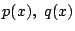 は一般的に
は一般的に
と表される.
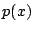 の次数が最小であるのは
の次数が最小であるのは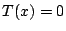 のときで
のときで
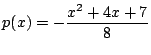 ,
,
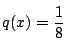 である.
である.
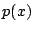 の最高次数の項の係数が1であるなかで,次数が最小であるのは,
の最高次数の項の係数が1であるなかで,次数が最小であるのは,
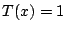 のときで
のときで
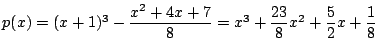 .
.
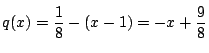 である.
である.
Aozora Gakuen
![]() ,
,![]() であるとき
であるとき
![]() は
は
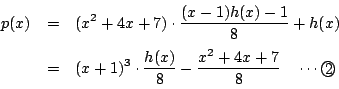
![]() の次数が最小であるのは
の次数が最小であるのは![]() のときで
のときで
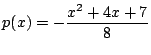 .
このとき
.
このとき
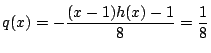 .
.
![]() の最高次数の項の係数が1であるなかで,次数が最小であるのは,
の最高次数の項の係数が1であるなかで,次数が最小であるのは,
![]() のときで
のときで
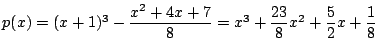 .
このとき
.
このとき
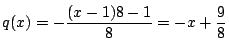 である.
である.
![]() の次数が最小であるのは
の次数が最小であるのは![]() のときで
のときで
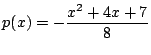 ,
,
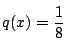 である.
である.
![]() の最高次数の項の係数が1であるなかで,次数が最小であるのは,
の最高次数の項の係数が1であるなかで,次数が最小であるのは,
![]() のときで
のときで
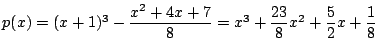 .
.
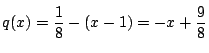 である.
である.