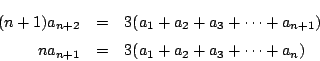次: 数列の公約数[86東工大]
上: 数学的帰納法か直接証明か
前: 数学的帰納法か直接証明か
次: 数列の公約数[86東工大]
上: 数学的帰納法か直接証明か
前: 数学的帰納法か直接証明か
問題
次のように定義される 数列 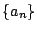 の一般項を求めよ.
の一般項を求めよ.
方針
-
- 1.
- 推測して数学的帰納法.
- 2.
- 和の処理による直説法.
解1
より
となるので
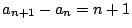 と推測できる.これから
と推測できる.これから 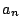 は
は
と推測される.
これを数学的帰納法で示す. 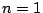 は成立.
は成立.
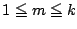 の範囲の
の範囲の 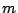 について
について
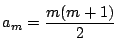 と仮定する.
と仮定する.
このとき
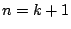 で成立し.すべての
で成立し.すべての  に対して
に対して
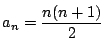 .
□
.
□
解2
より
つまり
両辺を
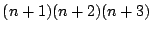 で割って
で割って
がすべての で成立する.
で成立する.
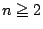 において
において
これは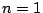 のときも含めて成立する.
□
のときも含めて成立する.
□
Aozora Gakuen
![]() の一般項を求めよ.
の一般項を求めよ.
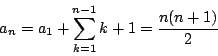
![]() は成立.
は成立.
![]() の範囲の
の範囲の ![]() について
について
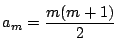 と仮定する.
と仮定する.
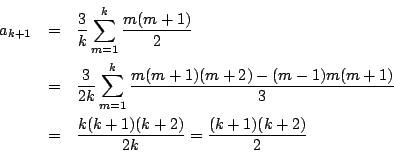
![]() で成立し.すべての
で成立し.すべての ![]() に対して
に対して
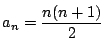 .
□
.
□