次: 整数値関数［08東工大理特］ 上: 数学的帰納法か直接証明か 前: 円周の分割［02東大文科］

有理数値関数［02京大後期理系改題］

問題     

$f(x)$ は $x^n$ の係数が1である $x$ の $n$ 次式である． 相異なる $n$ 個の有理数 $q_1,\ q_2,\ \cdots,\ q_n$に対して $f(q_1),\ f(q_2),\ \cdots,\ f(q_n)$がすべて有理数であれば， $f(x)$ の係数はすべて有理数であることを示せ．

方針

原題には「数学的帰納法を用いて」と指示があった． 方法を指定するのは問題としては良くないのでそれをとった．

1.

次数についての数学的帰納法

2.

$f(x)$を具体的に書き表す直接法

解1

$n=1$ のとき． $f(x)=x+b$ とおく．$f(q_1)=q_1+b$で$f(q_1)$ が有理数なので， $b=f(q_1)-q_1$ も有理数である．

$n=m$ のとき成立するとする．

$n=m+1$ のとき． $f(x)$ を $x^{m+1}$ の係数が1である $x$ の $m+1$ 次式とし， 相異なる $m+1$ 個の有理数 $q_1,\ q_2,\ \cdots,\ q_{m+1}$に対し $f(q_1),\ f(q_2),\ \cdots,\ f(q_{m+1})$がすべて有理数であるとする． 因数定理より

$$f(x)=(x-q_{m+1})Q(x)+f(q_{m+1}) \quad \cdots\maru{1}$$

となる．ここで $Q(x)$ は $m$ 次式で $x^m$ の係数は両辺の係数を比較して1である．

$q_1,\ q_2,\ \cdots,\ q_{m+1}$はすべて異なるので， $q_1,\ q_2,\ \cdots,\ q_m$に対し

$$Q(q_i)=\dfrac{f(q_i)-f(q_{m+1})}{q_i-q_{m+1}}$$

したがって $Q(q_1),\ \cdots,\ Q(q_m)$ はすべて有理数である．

数学的帰納法の仮定から $Q(x)$ は有理数係数の多項式である．ゆえに$\maru{1}$から $f(x)$ も 有理数係数の多項式である． したがって題意が示された．□

解2

$g(x)=f(x)-x^n$ は $n-1$ 次式である． $g(q_1),\ g(q_2),\ \cdots,\ g(q_n)$もすべて有理数である． $n-1$ 次式 $g(x)$ に対して$n$ 個の$x$に対する値が定まれば $g(x)$ は一意に定まる． 実際

$$\begin{eqnarray*} G(x)&=&g(q_1) \dfrac{(x-q_2)(x-q_3) \cdots (x-q_n)}{(q_1-q_... ...\cdots (x-q_{n-1})}{(q_n-q_1)(q_n-q_2) \cdots (q_n-q_{n-1})} \end{eqnarray*}$$

とおく．このとき $G(q_1)=g(q_1),\cdots,\ G(q_n)=g(q_n)$ なので恒等式の原理より $G(x)=g(x)$ ．したがって

$$\begin{eqnarray*} f(x)&=&x^n+g(x)\\ &=&x^n+g(q_1) \dfrac{(x-q_2)(x-q_3) \cdots ... ...\cdots (x-q_{n-1})}{(q_n-q_1)(q_n-q_2) \cdots (q_n-q_{n-1})} \end{eqnarray*}$$

これから $f(x)$ が有理数係数の $n$ 次多項式であることが示された．□

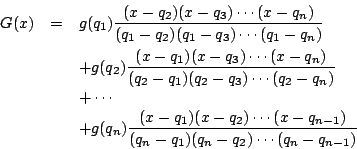
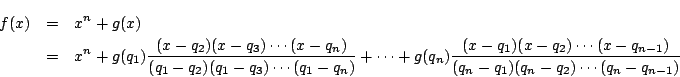
吟味

直接法は「ラグランジュの補間公式」の方法である． 最高次数の項の係数が1と指定されている$n$次式は，$n$個の値が決まれば１つに決まる． それを具体的に書き出すのが，補間公式である．