![]() を自然数,
を自然数,![]() を
を![]() 次多項式とする.
次多項式とする.
![]() が整数ならば,
すべての整数
が整数ならば,
すべての整数![]() に対し,
に対し,![]() は整数であることを証明せよ.
は整数であることを証明せよ.
方針
解法1
命題:が次多項式
において,
に対して
が整数ならば, すべての整数
に対し
は整数である.
![]() のとき.
のとき.![]() とおく.
とおく.![]() が整数なので,
任意の整数
が整数なので,
任意の整数![]() に対して
に対して![]() は整数である.
は整数である.
![]() に対して命題が成立するとし,
に対して命題が成立するとし,![]() のときの成立を示す.
のときの成立を示す.
![]() とおく.
とおく.
![\begin{eqnarray*}
P(x+1)-P(x)&=&a_n(x+1)^n-a_nx^n+[ n-1次以下の項のみ ] \\
&=&a_n(nx^{n-1}+\cdots)+[ n-1次以下の項のみ ]
\end{eqnarray*}](images/img495.gif)
![]() とおく.
とおく.
![]() は
は![]() 次以下で
次以下で
任意の整数![]() に対して
に対して![]() が整数であることを示す.
が整数であることを示す.
![]() なら条件から整数.
なら条件から整数.
![]() のとき.
のとき.![]() とおくと
とおくと
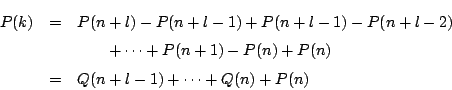
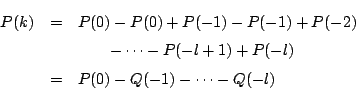
解法2
0以上の整数 ![]() に対し
に対し
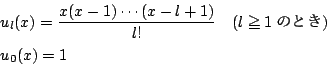
0以上の整数![]() に対し,
に対し,
![]() 次多項式
次多項式 ![]() は適当な実数
は適当な実数
![]() を用いて
を用いて
![]() のとき.
のとき. ![]() とすると
とすると![]() なので
なので![]() で
で
![]() となる.
となる.
![]() 以下のとき成立しているとする.
以下のとき成立しているとする.
![]() の
の ![]() の係数を
の係数を ![]() とする.
とする. ![]() とおく.このとき
とおく.このとき
以下,![]() は
は![]() のように表されているとする.
のように表されているとする.
![]() の範囲の
の範囲の![]() に対して
に対して![]() がすべて整数のとき,
がすべて整数のとき,
![]() が整数であることを数学的帰納法で示す.
が整数であることを数学的帰納法で示す.
![]() より
より![]() は整数.
は整数.
![]() のとき
のとき![]() であるから整数
であるから整数![]() に対して
に対して
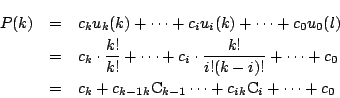
このとき,任意の整数![]() に対して
に対して![]() が整数であることを示す.
が整数であることを示す.
![]() なら条件から整数.
なら条件から整数.
![]() なら
なら
![]() なので
なので
![]() のとき
のとき ![]() とすると
とすると
解法3
![]() 次多項式
次多項式![]() の
の![]() 個の値
個の値
![]() を用いて
を用いて![]() 次式
次式![]() を
を
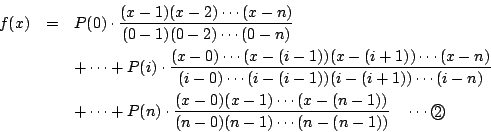
![]() と
と![]() は
は
![]() 個の相異なる
個の相異なる![]() の値
の値
![]() において同一の値
において同一の値
![]() をとる.
両式とも
をとる.
両式とも![]() の
の![]() 次式であるから,
次式であるから, ![]() は恒等式である.
は恒等式である.
よって![]() の右辺は
の右辺は![]() そのものである.
そのものである.
![]() のこの表示を用いて,
のこの表示を用いて,
![]() の
の![]() に対して
に対して![]() が整数のとき,
が整数のとき,
![]() の
の![]() に対しても
に対しても![]() が整数であることを示す.
が整数であることを示す.
そのためには各項
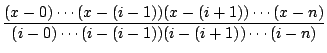 に
に
![]() を代入した値が整数であればよい.
を代入した値が整数であればよい.
![]() のとき.
のとき.
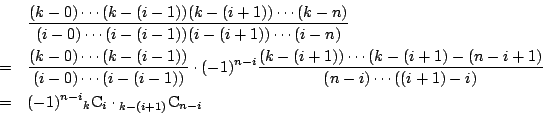
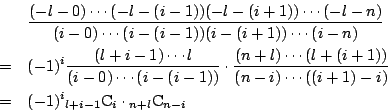
吟味
解法2は
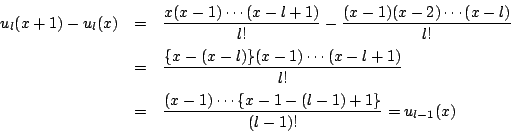
解法2の証明をよく見れば,
(1)の条件: ![]() 連続整数で
連続整数で ![]() が整数値を取ること
が整数値を取ること
(2)の条件:
![]() がすべて整数であること
がすべて整数であること
の同値性を直接示すこともできる.