

 次: 連立三角方程式[66静岡大]
上: 関数と方程式・不等式
前: 関数と方程式・不等式
次: 連立三角方程式[66静岡大]
上: 関数と方程式・不等式
前: 関数と方程式・不等式
問題

方針


解1
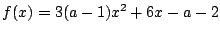 とおく.
とおく.
である.
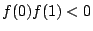 ,つまり
,つまり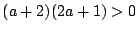 のとき,
中間値の定理から方程式
のとき,
中間値の定理から方程式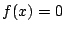 は
は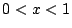 に解をもつ.
に解をもつ.
-
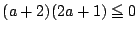 のとき.つまり
のとき.つまり
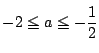 のとき.
のとき.
放物線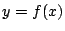 は上に凸であり,
は上に凸であり,
である.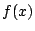 の判別式を
の判別式を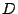 とすると
とすると
さらにこの範囲の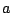 に対し
に対し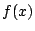 の軸
の軸
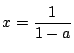 は
は
にある.したがって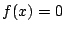 は区間
は区間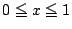 に2実数解をもち,
に2実数解をもち,
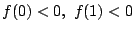 の少なくとも一方が成立するので,
の少なくとも一方が成立するので,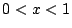 に少なくとも1つの実数解をもつ.
に少なくとも1つの実数解をもつ.
(i), (ii)より方程式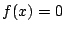 は
は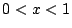 に少なくとも1つの実数解をもつ.
に少なくとも1つの実数解をもつ.
解2
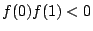 のときまでは解1.と同じ.
のときまでは解1.と同じ.
-
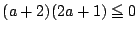 のとき.
つまり
のとき.
つまり
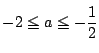 のとき.
のとき.
放物線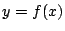 は上に凸であり,
は上に凸であり,
である.よって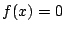 は区間
は区間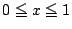 に2実数解をもち,
に2実数解をもち,
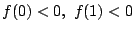 の少なくとも一方が成立するので,
の少なくとも一方が成立するので,
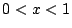 に少なくとも1つの実数解をもつ.
に少なくとも1つの実数解をもつ.
解3
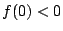 は
は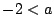 と,
と,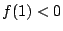 は
は
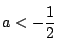 とそれぞれ同値である.
とそれぞれ同値である.
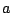 の2つの範囲をあわせると実数全体になるので,任意の実数
の2つの範囲をあわせると実数全体になるので,任意の実数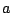 に対して
に対して
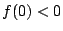 または
または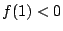 の少なくとも一方が成立する.
の少なくとも一方が成立する.
から
したがって
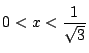 または
または
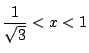 の少なくとも一方の区間に
の少なくとも一方の区間に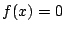 は解をもつ.
は解をもつ.
解4
区間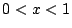 で
で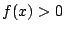 または
または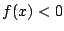 なら
なら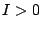 または
または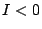 となり,
となり,
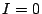 に矛盾する.
に矛盾する.
よって方程式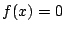 は
は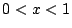 に少なくとも1つの実数解をもつ.
に少なくとも1つの実数解をもつ.
吟味
- 1.
- これはいちばん標準的な解法である.
その場合でも先に区間の端点の符号を調べておく方が簡明である.
- 2.
- 2次関数の場合,
多くは区間の中点の符号で判断できる.これは知っておきたい.
- 3.
- 任意の
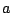 で成立するのだから,
で成立するのだから,
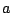 に関係ない
に関係ない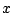 の値を調べようとした.
の値を調べようとした.
- 4.
- これは
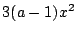 という形から試したのだ.
問題作成の舞台裏である.
という形から試したのだ.
問題作成の舞台裏である.



次: 連立三角方程式[66静岡大]
上: 関数と方程式・不等式
前: 関数と方程式・不等式
Aozora Gakuen




![]() とおく.
とおく.
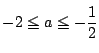 のとき.
のとき.
![]() は上に凸であり,
は上に凸であり,
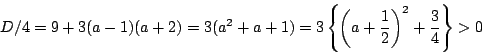
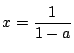 は
は
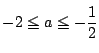 のとき.
のとき.
![]() は
は![]() と,
と,![]() は
は
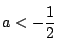 とそれぞれ同値である.
とそれぞれ同値である.
![]() の2つの範囲をあわせると実数全体になるので,任意の実数
の2つの範囲をあわせると実数全体になるので,任意の実数![]() に対して
に対して
![]() または
または![]() の少なくとも一方が成立する.
の少なくとも一方が成立する.
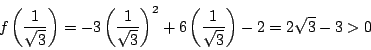
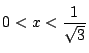 または
または
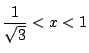 の少なくとも一方の区間に
の少なくとも一方の区間に![]() は
は![]() に少なくとも1つの実数解をもつ.
に少なくとも1つの実数解をもつ.