

 次: 不等式の証明[04明治大]
上: 関数と方程式・不等式
前: 方程式の解[88お茶の水]
次: 不等式の証明[04明治大]
上: 関数と方程式・不等式
前: 方程式の解[88お茶の水]
問題
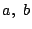 を実数として
を実数として
をともに満足させる実数 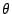 が存在するとき,
が存在するとき,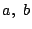 の満たすべき条件を求めよ.
の満たすべき条件を求めよ.
方針
- 1.
- 三角関数の連立方程式の問題として解ける.
- 2.
- この連立方程式の2式は
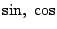 に関して同じ形をしている.
ド・モアブルの定理という,昨今は習わないが,複素数の三角関数表示を用いることで,
複素数の実部と虚部と見なす方が自然だ.
に関して同じ形をしている.
ド・モアブルの定理という,昨今は習わないが,複素数の三角関数表示を用いることで,
複素数の実部と虚部と見なす方が自然だ.
解1
第2式から
これから
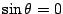 の場合.整数
の場合.整数  で
で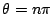 とかける.
とかける.
これが第1式をみたせばよい.
-
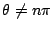 で
で
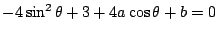 の場合.
の場合.
この式は
となる.また,連立方程式の第1式は
と変形できるので,この2式から
が得られる.つまり解があるとしたらそれは
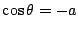 .これを
.これを
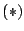 に代入して
に代入して 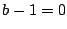 を得る.
を得る.
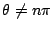 の
の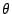 が存在するために
が存在するために
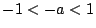 .つまり
.つまり 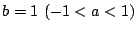 .
.
以上あわせて,求める 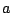 と
と 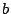 の条件は,
の条件は,
□
解2
したがって二次方程式
が絶対値1の解をもてば,それに対して 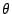 が定まる.
が定まる.
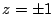 が解になるときは
が解になるときは 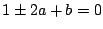 .
.
虚数解 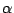 をもつときは,判別式の条件から
をもつときは,判別式の条件から 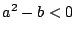 .
.
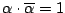 から
から 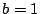 .したがってまた
.したがってまた 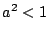
あわせて
□
吟味
このように,三角関数の計算なしにできてしまう.
本問は,実は私が高3のときに学校で使っていた問題集に載っていた問題だ.
演習の時間にこの問題があたった人は解1の方法で解いて黒板に書いていた.
私は解2のようにやった.黒板の解を見て,それよりもっと簡単にできるのに,
と思ったことを覚えている.その解を書いた級友の名前や教室の情景を今も
そこだけ切り取ったようにくっきりと覚えているので,この解2は自分自身にも印象深かった
のだと思う.
複素数では
なので,連立方程式を複素数一つの式にできる.その結果
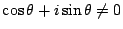 が使え,2次方程式の問題になってしまう.
連立三角方程式ではこの方法が有効なときがある.
が使え,2次方程式の問題になってしまう.
連立三角方程式ではこの方法が有効なときがある.
しかしさらに考えれば,これはそれほど別な解というわけではない.
加法定理
と,複素数の等式
は同等だ.
この同等性が根拠になって,加法定理の計算がド・モアブルの定理の中に吸收され,三角関数の計算がないように見えているだけのことだ.
別解といっても同じ根っこから出てきた別解である.
私は高校生のときはまったく違う解法だと思っていた.



次: 不等式の証明[04明治大]
上: 関数と方程式・不等式
前: 方程式の解[91お茶の水]
Aozora Gakuen
![]() を実数として
を実数として
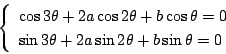
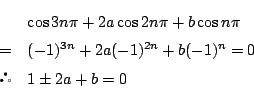
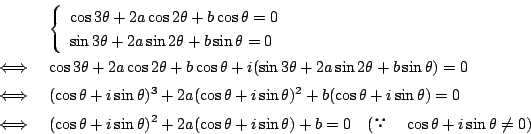
![]() が解になるときは
が解になるときは ![]() .
.
![]() をもつときは,判別式の条件から
をもつときは,判別式の条件から ![]() .
.
![]() から
から ![]() .したがってまた
.したがってまた ![]()
