相異なる3数 ![]() が
が
を満たすとき,次の式の値を求めよ.
例題 2.1 [84防衛大改題]
相異なる3数 ![]() が
が
考え方
問題の条件は三つの分数式の値が等しいといっている.
![]() 三つの文字に対して等式は二つだから
三つの文字に対して等式は二つだから
![]() の値が定まるわけではない.
しかし一定の式の値は定まる.それを求めよといっている.
三つ以上のものが等しい場合は,その式の値を文字におく.
互いに等しい値を文字におくのだ.
これは等しいものを文字におく典型だ.
そして得られた式を見れば,
の値が定まるわけではない.
しかし一定の式の値は定まる.それを求めよといっている.
三つ以上のものが等しい場合は,その式の値を文字におく.
互いに等しい値を文字におくのだ.
これは等しいものを文字におく典型だ.
そして得られた式を見れば,![]() について同じ形をしている.
これはどういうことか.そこから解答作りがはじまる.
について同じ形をしている.
これはどういうことか.そこから解答作りがはじまる.
解答
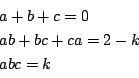
最初に等しいものを一つの文字に置くことがカギである. なお,解と係数を用いて関係式を導いたところは, 次のように辺々引いて求めていくこともできる.
解答2
(2.1)の第1式と第2式,第2式と第3式をそれぞれ引くと
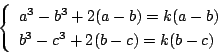
(2.1) の三式をすべて加えると
(2.2)式と
![]() の三式を加えると
の三式を加えると
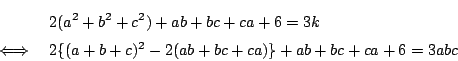
もしこの![]() とおく方法を使わず,
与えられた関係式のみから求めると,やや複雑になる.
とおく方法を使わず,
与えられた関係式のみから求めると,やや複雑になる.
解答3
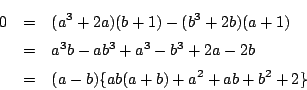
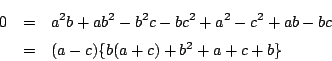
(2.3)に![]() を代入して
を代入して
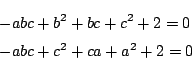
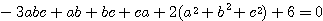
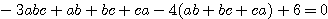
これは簡単な例であるが,三通りの方法で解くことができた. このようにひとつの解法が見つかっても, それで終わりにせずに他の解法はないか,考えてみたい. 異なる問題を三題解くよりも, 同じ問題を三通りの方法で解く方が力がつく.