四角形![]() が,半径
が,半径![]() の円に内接している.
この四角形の周の長さが44で,
辺
の円に内接している.
この四角形の周の長さが44で,
辺![]() と辺
と辺![]() の長さがいずれも13であるとき,
残りの2辺
の長さがいずれも13であるとき,
残りの2辺![]() と
と![]() の長さを求めよ.
の長さを求めよ.
例題 2.2 [06東大文科1番]
四角形![]() が,半径
が,半径![]() の円に内接している.
この四角形の周の長さが44で,
辺
の円に内接している.
この四角形の周の長さが44で,
辺![]() と辺
と辺![]() の長さがいずれも13であるとき,
残りの2辺
の長さがいずれも13であるとき,
残りの2辺![]() と
と![]() の長さを求めよ.
の長さを求めよ.
考え方 四角形が円に内接しているということは,それを分けた各三角形も円に内接している.正弦定理は外接円の半径と三角形の内角を用いて辺の長さを表す.二辺が既知の三角形で余弦定理と連立すれば,内角の正弦や余弦,残る辺の長さが決まる.それを,辺の長さが未知の方の三角形に用いればよい.
解答
![]() とする.
また
とする.
また![]() とする.このとき
とする.このとき
![]() である.
である.
![]() の外接円の半径が
の外接円の半径が![]() で
あるから,正弦定理によって
で
あるから,正弦定理によって
また
![]() に余弦定理を適用して,
に余弦定理を適用して,
![]() から
から![]() を消去する.
を消去する.
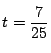 である.この結果
である.この結果
次に,
![]() において余弦定理を用いる.
において余弦定理を用いる.
![]() であるから
であるから