![]() を自然数とし,
を自然数とし,![]() または
または ![]() を
を
![]() 個並べた数列
個並べた数列
![]() を考える.例えば,
を考える.例えば, ![]() のときは
のときは
の4通りがある.
-
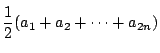 は整数であることを示せ.
は整数であることを示せ.
-
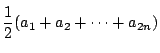 が2の倍数となるような
数列
が2の倍数となるような
数列
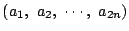 は全部で何通りあるか.
は全部で何通りあるか.
例題 2.15 [01愛媛大]
![]() を自然数とし,
を自然数とし,![]() または
または ![]() を
を
![]() 個並べた数列
個並べた数列
![]() を考える.例えば,
を考える.例えば, ![]() のときは
のときは
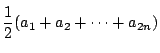 は整数であることを示せ.
は整数であることを示せ.
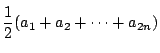 が2の倍数となるような
数列
が2の倍数となるような
数列
これは出題者が例( ![]() の場合)で考えなさいと言ってくれている.
の場合)で考えなさいと言ってくれている.
![]() のときは四つの場合,
のときは四つの場合,![]() は 0 か 2 か
は 0 か 2 か![]() のいずれかで,
つねに偶数になる.
任意の
のいずれかで,
つねに偶数になる.
任意の ![]() に対しどのように考えればよいか.
そこを考える.
に対しどのように考えればよいか.
そこを考える.
(2)はどのように考えるか.
(1)の考え方をふまえると![]() が4の倍数になるような数列の総数ということになる.
が4の倍数になるような数列の総数ということになる.
解答
(1)
![]() の中で,
1と
の中で,
1と![]() を可能なだけ組にする.
を可能なだけ組にする.
![]() 組できたとする.
すると殘りは
組できたとする.
すると殘りは ![]() 個で,
これらはすべて1か
個で,
これらはすべて1か![]() である.したがってその和は
である.したがってその和は ![]() または
または ![]() となり,つねに偶数である.
となり,つねに偶数である.
(2) 1の個数が
![]() である数列は
である数列は![]() 通りできる.このとき-1は
通りできる.このとき-1は 個あるので和は
個あるので和は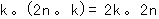 である.
である. が4の倍数になればよい.
が4の倍数になればよい.
![]() が偶数か奇数かで場合に分ける.
が偶数か奇数かで場合に分ける.
![]() のとき
のとき![]() なので
なので![]() が4の倍数になるのは
が4の倍数になるのは
![]() が偶数のとき.
が偶数のとき.
![]() のとき
のとき
![]() なので
なので
![]() が4の倍数になるのは
が4の倍数になるのは
![]() が奇数のとき.
ところが
二項定理
が奇数のとき.
ところが
二項定理
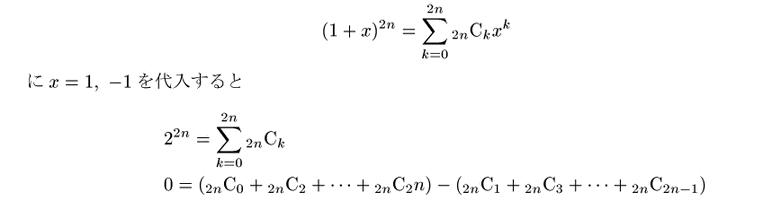
これから
例を考えると話しが具体的になり, 抽象的な証明も何をやっているかよくわかる.