![]() ,
,
![]() が整数のとき,任意の自然数
が整数のとき,任意の自然数 ![]() に対して
に対して
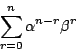
は整数であることを示せ.
例題 1.10 [出典不明]
![]() ,
,
![]() が整数のとき,任意の自然数
が整数のとき,任意の自然数 ![]() に対して
に対して
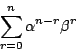
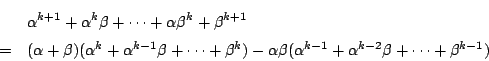
となる.仮定したのは ![]() のときなので,第二のかっこ内が整数である保証がない.
このようなときは[応用型1]になる.
つまり次のようにする.
のときなので,第二のかっこ内が整数である保証がない.
このようなときは[応用型1]になる.
つまり次のようにする.
解答
数学的帰納法で示す.
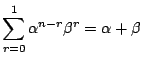 で成立.
で成立.
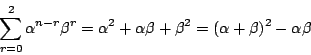
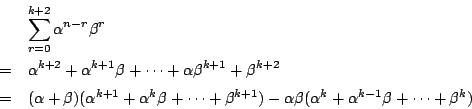
例題 1.11 [00横浜国立大学改題]
数列 ![]() を
を
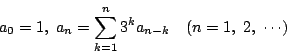
考え方
このようになかなか解けない数列の一般項を求めたいときは,
いくつかの ![]() について調べ,一般項を推測するところからはじめなければならない.
について調べ,一般項を推測するところからはじめなければならない.
解答
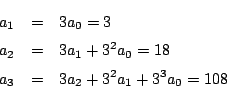
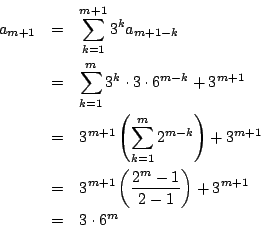
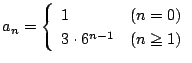 である.
□
である.
□
![]() だからといって
だからといって