![]() とする.
とする.![]() 個の実数
個の実数
![]() は
は
![]() をみたしている.
このとき,
をみたしている.
このとき,
考え方
この問題の ![]() と
と
![]() は本来,
出題者の与えた定数であり,固定されている.
しかし,ここで証明すべきことを次のような命題にする.
は本来,
出題者の与えた定数であり,固定されている.
しかし,ここで証明すべきことを次のような命題にする.
解答 次の命題を示せばよい.
とする.
個の実数
が,条件
をみたすならば, 不等式
がなり立つ.これを数学的帰納法で示す.
![]() 個の実数の条件
個の実数の条件
![]() ,
と,
条件
,
と,
条件
![]() がある.これからつくられた自然数
がある.これからつくられた自然数![]() に関する条件
に関する条件
このようにしておくと,数学的帰納法の仮定が,
個別の ![]() に対して仮定されるのではなく,
条件を満たす任意の
に対して仮定されるのではなく,
条件を満たす任意の ![]() に対して仮定されるので,
証明がずっとやりやすくなる.
「証明すべきことを強める」とか「個数に関する数学的帰納法」
とかいろいろ呼ばれる.
基本は自然数
に対して仮定されるので,
証明がずっとやりやすくなる.
「証明すべきことを強める」とか「個数に関する数学的帰納法」
とかいろいろ呼ばれる.
基本は自然数![]() を含む命題の成立を,
を含む命題の成立を,
![]() についての数学的帰納法で示すのである.
個別の
についての数学的帰納法で示すのである.
個別の ![]() とはいっても文字
とはいっても文字 ![]() であるから,
もともとの命題そのものを強めた意味で
解釈することもできる.
要はどのような数学的帰納法をしているのか,明確に押さえることである.
であるから,
もともとの命題そのものを強めた意味で
解釈することもできる.
要はどのような数学的帰納法をしているのか,明確に押さえることである.
例題 1.13 [97東京工大改題]
![]() を自然数,
を自然数, ![]() を正の有理数とする.このとき,
を正の有理数とする.このとき,
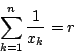
考え方
![]() 個の未知数とある与えられた有理数
個の未知数とある与えられた有理数 ![]() に関する命題,
を証明するのに,これを
に関する命題,
を証明するのに,これを
解答
「未知数の個数が ![]() であるかぎり,
任意の有理数
であるかぎり,
任意の有理数 ![]() について,解の個数が有限個である」
ことを数学的帰納法で証明する.
について,解の個数が有限個である」
ことを数学的帰納法で証明する.
まず,任意の有理数 ![]() に対して
に対して
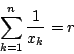
![]() とする.
とする.
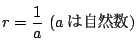 という形をしているときは,
という形をしているときは,
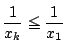 であるから
であるから
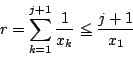
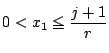 となりこれを満たす整数
となりこれを満たす整数 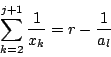
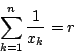
従って,題意の有限性が証明された.□
このように, ![]() 以外にも定数などがある場合に,証明することを強めることによって,
帰納法がかえってうまくできることが少なくない.
以外にも定数などがある場合に,証明することを強めることによって,
帰納法がかえってうまくできることが少なくない.