次: 問題と考え方 上: 間接証明と背理法 前: 背理法

ある間接証明

次の問題は直接示すこともできるが，本質的には間接証明だ．

例題 1.19       ［09京大理系乙］

平面上の鋭角三角形 $\bigtriangleup \mathrm{ABC}$の内部（辺や頂点は含まない）に点Pをとり， $\mathrm{A}'$をB，C，Pを通る円の中心， $\mathrm{B}'$をC，A，Pを通る円の中心， $\mathrm{C}'$をA，B，Pを通る円の中心とする． このときA，B，C， $\mathrm{A}',\ \mathrm{B}',\ \mathrm{C}$が同一円周上にあるための 必要十分条件はPが $\bigtriangleup \mathrm{ABC}$の内心に一致することであることを示せ．

考え方    

中心が同一直線上にない三円が同一の点を共有すれば， その点は一つしかない．あるいは，三角形の外心はただ一つしかない． この簡単なことを用いると，間接証明ができる．

証明    

点$\mathrm{P}$と $\mathrm{A}',\ \mathrm{B}',\ \mathrm{C}'$が題意のように定まっている 前提のもとで次の二条件の同値性を示す．

条件甲：A，B，C， $\mathrm{A}',\ \mathrm{B}',\ \mathrm{C}'$が同一円周上にある．

条件乙：Pが $\bigtriangleup \mathrm{ABC}$の内心$\mathrm{I}$と一致する．

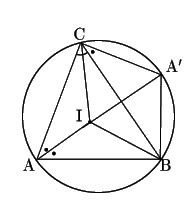(1)甲ならば乙を示す．

     $\mathrm{A'B}=\mathrm{A'C}$より$\mathrm{A}'$は弧$\mathrm{BC}$の中点． 円周角の相等より $\angle \mathrm{A'AB}=\angle \mathrm{A'AC}$． つまり直線$\mathrm{AA'}$は角$A$の二等分線である． 従って内心$\mathrm{I}$は$\mathrm{AA'}$上にある． 他についても同様なので，三直線 $\mathrm{AA'},\ \mathrm{BB'},\ \mathrm{CC'}$は 内心$\mathrm{I}$で交わる．

     $\angle \mathrm{CIA'}=\angle \mathrm{IAC}+\angle \mathrm{ICA},\ \angle \mathrm{ICA'}=\angle \mathrm{ICB}+\angle \mathrm{BCA'}$ である．

    ここで 角の二等分より $\angle \mathrm{ICA}=\angle \mathrm{ICB}$． 円周角の相等によって $\angle \mathrm{BCA'}=\angle \mathrm{BAA'}=\angle \mathrm{IAC}$． これから $\angle \mathrm{CIA'}=\angle \mathrm{ICA'}$が結論される．

    この結果 $\mathrm{A'I}=\mathrm{A'C}$となり，内心$\mathrm{I}$は$\mathrm{A}'$を中心とし $\mathrm{B},\ \mathrm{C}$を通る円周上にある．点$\mathrm{P}$も同じ円周上にある． $\mathrm{B'},\ \mathrm{C'}$についても同様に成り立つ．

三点 $\mathrm{A}',\ \mathrm{B}',\ \mathrm{C}'$ を中心とする三円上に$\mathrm{I}$と$\mathrm{P}$の両点がある． これら三円の中心が一直線上に来ることはない． よって三円が共有する点は一点しかない． つまり $\mathrm{P}=\mathrm{I}$である．

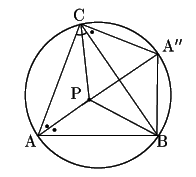(2)乙ならば甲を示す．

     $\angle \mathrm{A}$の二等分線と $\bigtriangleup \mathrm{ABC}$の外接円の交点を     $\mathrm{A}''$とする． 点$\mathrm{P}$は内心なので，(1)と同様にして， $\mathrm{PA''}=\mathrm{BA''}=\mathrm{CA''}$である．

    つまり$\mathrm{A}''$は三点 $\mathrm{P},\ \mathrm{B},\ \mathrm{C}$ から等距離にある．点$\mathrm{A}'$も等距離にある． 同一直線上にない三点から等距離にある点は一つなので $\mathrm{A}'=\mathrm{A}''$である．つまり $\mathrm{A}'$は $\bigtriangleup \mathrm{ABC}$の外接円上にある． 他も同様である． □