

 次: ある間接証明
上: 間接証明と背理法
前: 対偶を示す
次: ある間接証明
上: 間接証明と背理法
前: 対偶を示す
古来有名な背理法を振り返ろう.
これは昔から知られていることを入試問題にしたものだ.
解答を作ってみてほしい.
例題 1.15
[00北見工業大学]
解答
-
- (1)
- 背理法
- (2)
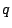 は
は
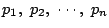 のどれで割っても 1 余るからである.
のどれで割っても 1 余るからである.
- (3)
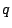 は
は
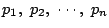 を因数にもたない1より大きい整数なので,
その素因数は
を因数にもたない1より大きい整数なので,
その素因数は
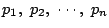 と異なる.
よって
と異なる.
よって
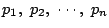 がすべての素数であるという仮定と矛盾する.
がすべての素数であるという仮定と矛盾する.
- (4)
-
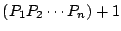 は
は
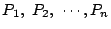 を因数にもたない
1より大きい整数なので,その素因数
を因数にもたない
1より大きい整数なので,その素因数 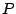 は
は
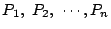 と異なる.
と異なる.
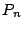 は小さい方から
は小さい方から  番目の素数なので
番目の素数なので
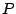 は
は
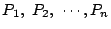 より大きい.
より大きい.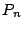 の次に大きいのが
の次に大きいのが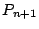 なので
なので
よって題意が示された.□
証明がこのようにできる以上,
その証明の前提となる条件がなければならない.
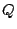 を「素数は無数にある」という命題として
この問題を「
を「素数は無数にある」という命題として
この問題を「 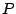 ならば
ならば 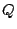 」の形にするとき
」の形にするとき 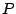 には何が来るのだろう.
には何が来るのだろう.
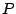 としてはこの場合「『素数』を1とそれ自身の他に約数のない数と定める」
という定義命題がとれる.つまりこの証明のなかには素数の定義が前提として入っている.
としてはこの場合「『素数』を1とそれ自身の他に約数のない数と定める」
という定義命題がとれる.つまりこの証明のなかには素数の定義が前提として入っている.
この証明は本質的にはユークリッドによってなされた.
ユークリッドは『原論』のなかで,
素数の個数が三個であるとして矛盾が起こるという形で議論した.
ユークリッドは歴史に残る人のなかで,はじめて背理法を用いた人である.
次の命題も,
その証明は背理法の典型であるが,背理法の立て方はいくつかある.
例題 1.16
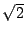 が無理数であることを示せ.
が無理数であることを示せ.
解答1
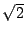 が無理数でない,つまり有理数とする.
が無理数でない,つまり有理数とする.
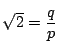 とおく.ここで分数を約分し
とおく.ここで分数を約分し 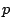 と
と 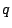 は互いに素であるとする.
は互いに素であるとする.
奇数の平方は再び奇数であるから左辺が偶数なので 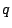 は偶数でなければならない.
は偶数でなければならない. 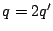 とおく.すると
とおく.すると
これから 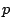 も偶数となり,
も偶数となり, 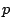 と
と 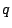 が互いに素であることと矛盾した.
ゆえに
が互いに素であることと矛盾した.
ゆえに 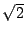 は無理数である.□
は無理数である.□
解答2
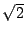 が無理数でない,つまり有理数とする.
が無理数でない,つまり有理数とする.
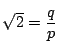 とおく.
とおく.
左辺の因数分解における因数2の個数は奇数である.
右辺の因数分解における因数2の個数は偶数である
これは矛盾である.
ゆえに 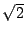 は無理数である.□
は無理数である.□
解答3
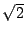 が無理数でない,つまり有理数とする.
が無理数でない,つまり有理数とする.
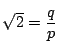 とおく.
とおく.
奇数の平方は再び奇数であるから左辺が偶数なので 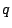 は偶数でなければならない.
は偶数でなければならない. 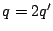 とおく.すると
とおく.すると
これから 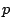 も偶数となり
も偶数となり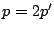 とおける.これから再び
とおける.これから再び
となる.再び 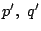 とも2で割れる.これは何回でも繰り返される.
つまり
とも2で割れる.これは何回でも繰り返される.
つまり 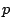 も
も 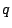 も2で無限回割れる.これは
も2で無限回割れる.これは 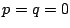 以外では不可能である.
ゆえに
以外では不可能である.
ゆえに 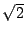 は無理数である.□
は無理数である.□
「 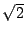 は無理数である」という命題は「
は無理数である」という命題は「 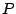 ならば
ならば 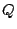 」という形はしていない.
」という形はしていない.
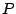 のところは少なくとも,
無理数の定義,整数,有理数の定義と性質が入っていなければならない.
が,それは当然の前提として命題中には書かれていない.
したがって,有理数のどのような性質との矛盾を導くのかによって,いくつかの解法がある.
のところは少なくとも,
無理数の定義,整数,有理数の定義と性質が入っていなければならない.
が,それは当然の前提として命題中には書かれていない.
したがって,有理数のどのような性質との矛盾を導くのかによって,いくつかの解法がある.
例題 1.17
[大阪市大]
解答
(1)
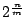 が有理数と仮定し,既約分数
が有理数と仮定し,既約分数
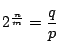 とおく.これから
とおく.これから
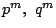 も互いに素で2が素数なので
も互いに素で2が素数なので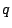 は2の倍数である.
は2の倍数である.
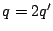 とおく.これを代入し簡約すると
とおく.これを代入し簡約すると
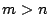 なので右辺は偶数.この結果
なので右辺は偶数.この結果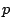 も2の倍数となり,
も2の倍数となり,
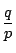 が既約分数であること矛盾した.
が既約分数であること矛盾した.
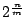 を有理数と仮定するかぎり起こる矛盾なので,
を有理数と仮定するかぎり起こる矛盾なので,
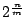 は有理数でない,つまり無理数である.
は有理数でない,つまり無理数である.
(2)
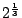 は3次方程式
は3次方程式
の解である.さらに
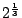 が有理数係数の2次方程式の解でもあるとする.2次方程式の
が有理数係数の2次方程式の解でもあるとする.2次方程式の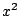 の係数で割ることにより
の係数で割ることにより
の解であるとしてよい.
ここで
である.ここに
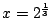 を代入することにより
を代入することにより
となる.
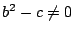 なら
なら
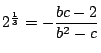 となる.
(1)を
となる.
(1)を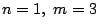 で用いると
で用いると
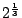 は無理数なので,矛盾である.
は無理数なので,矛盾である.
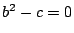 なら
なら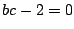 も成り立ち,
も成り立ち,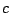 を消去して
を消去して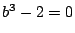 .
.
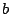 は実数なので
は実数なので
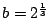 となり,
となり,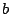 が有理数であることと矛盾した.
が有理数であることと矛盾した.
したがって
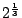 は有理数を係数とする2次方程式の解にならないことが示された.
□
は有理数を係数とする2次方程式の解にならないことが示された.
□
次の例題もまたいろんな証明法がある.
例題 1.18
[名大類題]
解答1
(1)
背理法で示す.
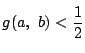 とする. つまり,
とする. つまり, 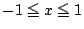 のすべての
のすべての 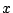 に対して,
に対して,
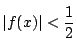 が成り立つとする.
特に
が成り立つとする.
特に
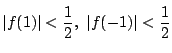 であるから
であるから
つまり
を得る. 辺々加えると
つまり
しかし, これは
を意味するので, 仮定と矛盾.
よって,
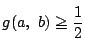 が示された.
が示された.
(2)
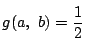 のとき
のとき 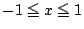 のすべての
のすべての
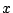 に対して,
に対して,
 が成り立つ.
が成り立つ.
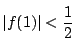 または
または
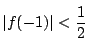 の少なくとも一方が成り立つと,
(1)と同様に
の少なくとも一方が成り立つと,
(1)と同様に
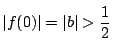 となる.
これは,
となる.
これは,
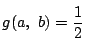 に反する.
よって
に反する.
よって
である. ここで, もし
とすると,
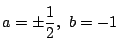 になる.
この場合
になる.
この場合
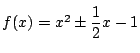 となり
となり 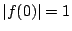 で不適.
で不適.
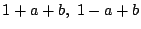 がともに負となるときも, 明らかに不適.
よって
がともに負となるときも, 明らかに不適.
よって
が必要である.
このとき,
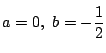 となり,
となり,
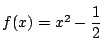 となるので,
確かに,
となるので,
確かに,
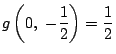 である.
である.
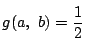 となる
となる 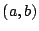 はこれにかぎることも示された.
□
はこれにかぎることも示された.
□
解答2
(1)
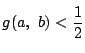 とする.
つまり,
とする.
つまり, 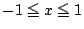 のすべての
のすべての 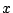 に対して,
に対して,
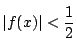 が成り立つとする.
特に
が成り立つとする.
特に
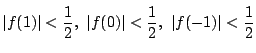 であるから
であるから
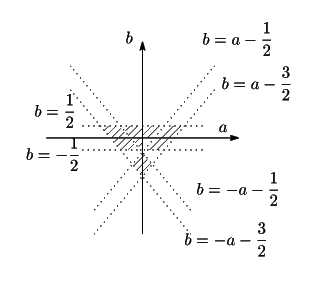 この領域を
この領域を 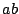 平面に図示する.
平面に図示する.
の領域と,
領域
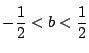 には共通部分がない.
には共通部分がない.
これは関数 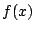 が与えられている,
つまり存在していることと矛盾する.
が与えられている,
つまり存在していることと矛盾する.
よって,
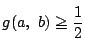 が示された.
が示された.
(2)
としたとき,これらの条件をみたすのは図から明らかに
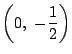 のみ.□
のみ.□
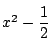 という関数を既知であれば次のような論証が可能である.
という関数を既知であれば次のような論証が可能である.
解答3
(1)
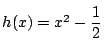 とおく.
これを用いて,
とおく.
これを用いて,
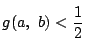 として矛盾を示す.
として矛盾を示す.
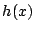 は
は 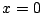 で最小値
で最小値
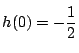 をとり,
をとり,
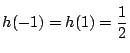 である.
である.
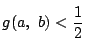 であるから
であるから
したがって 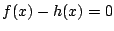 は
は 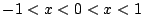 におのおの一個,
合計二個の解を持つ.ところが
におのおの一個,
合計二個の解を持つ.ところが
となり,一次式であるから,恒等的に 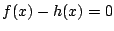 が成り立つ.
つまり
が成り立つ.
つまり
ところが 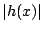 は
は 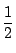 の値をとる.
すなわち
の値をとる.
すなわち
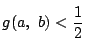 と矛盾した.
と矛盾した.
したがって
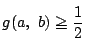 .
.
(2)
(1)より
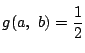 になるのが
になるのが
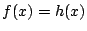 のときだから
のときだから
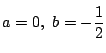 .
.
つまり
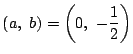 .
□
.
□


 次: ある間接証明
上: 間接証明と背理法
前: 対偶を示す
Aozora Gakuen
次: ある間接証明
上: 間接証明と背理法
前: 対偶を示す
Aozora Gakuen
![]() とする.
このとき,
とする.
このとき,
![]() を考えると,
を考えると,
![]() は
は
![]() のどれでも割り切れない.
のどれでも割り切れない.![]() したがって,
したがって, ![]() を素数の積として表したとき,
この積に現れる素数は
を素数の積として表したとき,
この積に現れる素数は
![]() のいずれとも異なる.
これは矛盾である.
のいずれとも異なる.
これは矛盾である.![]() したがって定理が証明された.
したがって定理が証明された.
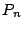 で小さい方から
で小さい方から  番目の素数を表すとき,不等式
番目の素数を表すとき,不等式
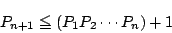
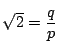 とおく.ここで分数を約分し
とおく.ここで分数を約分し 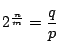 とおく.これから
とおく.これから
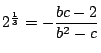 となる.
(1)を
となる.
(1)を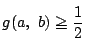 を示せ.
を示せ.
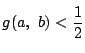 とする. つまり,
とする. つまり, 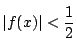 が成り立つとする.
特に
が成り立つとする.
特に
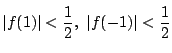 であるから
であるから
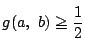 が示された.
が示された.
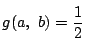 のとき
のとき  が成り立つ.
が成り立つ.
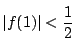 または
または
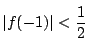 の少なくとも一方が成り立つと,
(1)と同様に
の少なくとも一方が成り立つと,
(1)と同様に
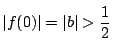 となる.
これは,
となる.
これは,
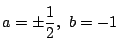 になる.
この場合
になる.
この場合
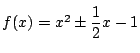 となり
となり 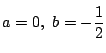 となり,
となり,
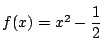 となるので,
確かに,
となるので,
確かに,
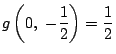 である.
である.
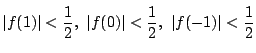 であるから
であるから
 この領域を
この領域を 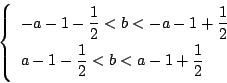
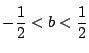 には共通部分がない.
には共通部分がない.
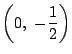 のみ.□
のみ.□
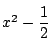 という関数を既知であれば次のような論証が可能である.
という関数を既知であれば次のような論証が可能である.
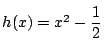 とおく.
これを用いて,
とおく.
これを用いて,
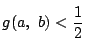 として矛盾を示す.
として矛盾を示す.
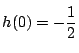 をとり,
をとり,
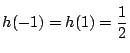 である.
である.
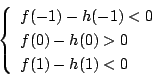
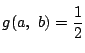 になるのが
になるのが
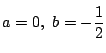 .
.
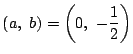 .
□
.
□