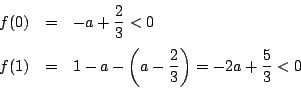次: 個数を数える場合分け
上: 場合分け
前: 場合分け
次: 個数を数える場合分け
上: 場合分け
前: 場合分け
これらを例題で考えながら,確認していこう.
例題 1.1
[00京大文系前期]
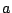 を実数とする.
を実数とする. 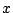 の二次方程式
の二次方程式
は
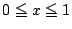
の範囲にいくつの解をもつか.
考え方
まず右辺の定積分を計算しなければならない.
被積分関数に絶対値がある.
絶対値記号はそれ自身場合分けで定義される記号だ.つまり
したがって次の所からはじめることになる.
解答
である.一方,積分域は 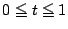 である.
である.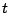 がこの範囲を動くとき,
途中で
がこの範囲を動くとき,
途中で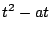 の符号が変わるか変わらないかは
の符号が変わるか変わらないかは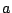 の範囲によって決まる.
の範囲によって決まる.
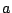 の範囲によって積分計算は次のように区間に分けねばならない.
の範囲によって積分計算は次のように区間に分けねばならない.
である.
注意
- このように場合分けではまず場合分けを済ますことが大切だ.
上の一つ一つについて,その場で計算する人もいるが,
先に全体の場合分けを済ますこと.
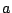 の範囲の境界での等号はいずれにつけてもよい.
境界ではいずれの式で計算しても同じ値になる.
の範囲の境界での等号はいずれにつけてもよい.
境界ではいずれの式で計算しても同じ値になる.
積分を計算して
となる.
そこで,
とおく. 区間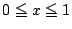 の端の値
の端の値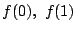 の符号を調べる.
の符号を調べる.
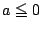 のとき
のとき
よって 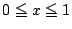 における解は1個.
における解は1個.
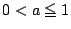 のとき
のとき
よってこの場合はさらに場合分けされる.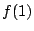 の値が0以上なら1個,0未満なら0個である.
の値が0以上なら1個,0未満なら0個である.
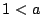 のとき
のとき
よって 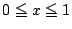 における解は0個.
における解は0個.
以上から与方程式の 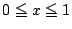 における解は
における解は
となる.
□
Aozora Gakuen
![]() を実数とする.
を実数とする. ![]() の二次方程式
の二次方程式
![]() を実数とする.
を実数とする. ![]() の二次方程式
の二次方程式
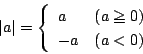
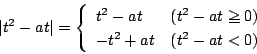
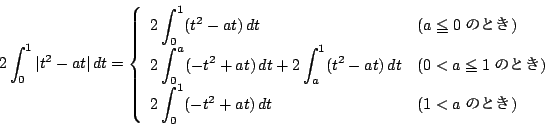
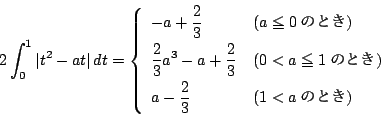
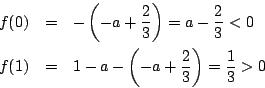
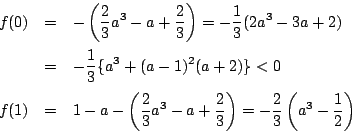
![\begin{displaymath}
\left\{
\begin{array}{ll}
1個&\left(0<a \le \dfrac{1}{\sq...
...ft(\dfrac{1}{\sqrt[3]{2}}<a \le 1\right)
\end{array} \right.
\end{displaymath}](images/img26.gif)