

 次: 問題と考え方
上: 場合分け
前: 定数の範囲で式が変わる
次: 問題と考え方
上: 場合分け
前: 定数の範囲で式が変わる
こんどは個数を数える場合分けをやってみよう.
ていねいに場合分けをしていこう.
例題 1.2
[鳥取大過去問]
ある試験において,20点満点の問題が5題出題されている.
各問いとも0点,5点,10点,15点,20点のいずれかで全部を採点するものとする.
-
- (1)
- おこりうる採点の仕方はいく通りあるか.
- (2)
- 少なくとも3問が正解である場合はいく通りあるか.
- (3)
- 総得点が80点以上である場合はいく通りあるか.
解答
-
- (1)
- 各問いとも5通りの採点の仕方があるから
- (2)
- 正解の個数で場合に分けて考えよう.
5問とも正解になるのは,1(通り)
4問正解になるのは
同様に3問正解になるのは
あわせて
- (3)
- まずどのような場合分けが必要かを考えよう.
得点で考えるのがよいか.
減点で考えるのがよいか.
問題1〜問題5の各々から減点される点数を
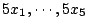 とする.
とする.
となる非負の整数
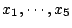 の取り方の総数が求めるものである.
の取り方の総数が求めるものである.
条件
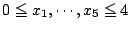 は
は
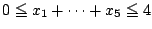 なら必然的に満たされる.
なら必然的に満たされる.
のとき
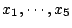 の取り方の総数は
の取り方の総数は
それぞれの場合の計算式ができた.
この場合分けはもちろん重なりがない.よって
となる.
□
別解
工夫をすれば場合分けが必要でなくなる.
となる非負整数の組
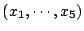 に対し
に対し
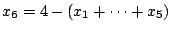 とすると
とすると
となる非負整数の組
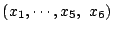 が得られる.
が得られる.
逆に
となる非負整数の組
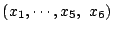 から
から
となる非負整数の組
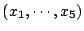 が得らる.
が得らる.
よってこれらはは1対1に対応している.
となる非負整数の組
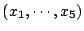 と
と
となる非負整数の組
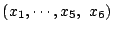 は同じだけある.
は同じだけある.
である.
□
次の問題はどのような場合分けが必要かはそれほど明らかではない.
例題 1.3
[08京大文系]
考え方
このようなときは「例で考える」にしたがって,
 の値を4や5で考えてみるのも一つの方法である.
頂点から頂点に移動するには辺と弧のいずれを先に描くかで2通り.
それに気づけば,
結局頂点をどの順に動いていくかという問題だということがわかる.
(2)では,
頂点間の移動が辺と弦の両方通れるときと,
一方しか通れないときがあることと,
ここにも場合分けの要素がこのようにあることがわかる.
の値を4や5で考えてみるのも一つの方法である.
頂点から頂点に移動するには辺と弧のいずれを先に描くかで2通り.
それに気づけば,
結局頂点をどの順に動いていくかという問題だということがわかる.
(2)では,
頂点間の移動が辺と弦の両方通れるときと,
一方しか通れないときがあることと,
ここにも場合分けの要素がこのようにあることがわかる.
一方, のときの場合の数を
のときの場合の数を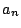 や
や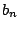 とおいて漸化式を立て求めることもできる..
とおいて漸化式を立て求めることもできる..
解答
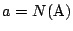 について.
一筆がきの経路に関する場合分けは次の様に起こる.
について.
一筆がきの経路に関する場合分けは次の様に起こる.
- 頂点から隣りあう頂点への移動は
 カ所あり,
それぞれ移り方は辺と弧のいずれを先に通るかの2通り.
したがって,頂点の間の移動の順を決めれば,それに対して経路は
カ所あり,
それぞれ移り方は辺と弧のいずれを先に通るかの2通り.
したがって,頂点の間の移動の順を決めれば,それに対して経路は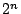 通りできる.
通りできる.
- 点の間の移動順では,右回りから始めるか,左回りから始めるかが場合分けされる.
これは対称性からたがいに同数あるので,左回りからはじめる場合で考えその2倍ある.
- 左回りからはじめるときで考える.
点の間の移動順では,途中で折り返さないか途中で折り返すかの場合に分けられる.
折り返さない場合は1通り.
折り返す場合.2回折り返すのはA以外で折り返すとき.Aで折り返すときは1回折り返す.
したがって折り返しなしも含めて,折り返しの仕方は
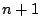 通り.
通り.
これらはそれぞれ異なる一筆がきを作り,場合分けは他にはない.
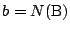 について.
について.
点Bのある辺をCDとする.左回りにC,B,Dと並ぶものとする.
点Bに始まり点Bに終わる一つの一筆がきに対し,
左回りなら最初のBDを書くところを最後に移動することでDから始まる一筆がきで,
最後にDに戻るとき辺を通るものが得られる.
右回りなら最初のBCを書くところを最後に移動することでCから始まる一筆がきで,
最後にCに戻るとき辺を通るものが得られる.
逆にこの操作を逆にたどることで,頂点を始点とする一筆がきで最後に始点に戻るとき辺を通るものから,
その辺の中点を始点とする一筆がきが得られ,これは一対一に対応している.
したがって,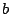 は頂点から始まる一筆がきで,
最後に始点に戻るとき辺を通ると指定した場合の数に等しい.
この条件を付け加えた頂点を始点とする一筆がきは
は頂点から始まる一筆がきで,
最後に始点に戻るとき辺を通ると指定した場合の数に等しい.
この条件を付け加えた頂点を始点とする一筆がきは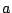 の計算で1.の部分を
の計算で1.の部分を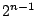 としたものである.
としたものである.
以上である.
□
別解
正 角形の代わりに凸な
角形の代わりに凸な 角形で考えても同じことである.
角形で考えても同じことである.
 角形のときの
角形のときの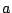 を
を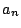 とする.
とする.
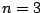 のとき,
左回りと決めると
のとき,
左回りと決めると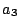 は点の移動の順番の決め方が4通りある.
一つの順番に対し,辺と弧の選び方は
は点の移動の順番の決め方が4通りある.
一つの順番に対し,辺と弧の選び方は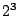 通りある.
右回りも同数.
ゆえに
通りある.
右回りも同数.
ゆえに
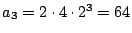 である.
である.
 角形に新たに
角形に新たに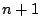 番の頂点を加えると,
その頂点を挟むもとの
番の頂点を加えると,
その頂点を挟むもとの 角形の2頂点の間の移動の仕方が,
2通りから4通りになる.
これによって
角形の2頂点の間の移動の仕方が,
2通りから4通りになる.
これによって 角形の場合の一つの一筆がきの経路に対し,
角形の場合の一つの一筆がきの経路に対し,
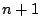 角形の場合の一筆がきの経路が2つ得られる.
角形の場合の一筆がきの経路が2つ得られる.
さらに新たに付け加わった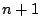 番目の点で折り返す一筆がきの経路が
右回りと左回りも考えて
番目の点で折り返す一筆がきの経路が
右回りと左回りも考えて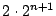 個できる.
ゆえに
個できる.
ゆえに
これから
これを整理して,
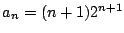 .
.
同様に
 角形のときの
角形のときの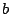 を
を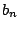 とする.
とする.
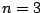 のとき,
左回りと決めると
のとき,
左回りと決めると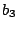 も点の移動の順番の決め方は4通りある.
一つの移動の型に対し,Bのある辺は,一筆がきの最初と最後が辺を通り,
途中では弧を通ることが決まるので,
も点の移動の順番の決め方は4通りある.
一つの移動の型に対し,Bのある辺は,一筆がきの最初と最後が辺を通り,
途中では弧を通ることが決まるので,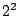 通りある.
通りある.
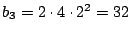 である.
である.
 角形に新たに
角形に新たに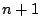 番の頂点を加えると,
その頂点を挟むもとの
番の頂点を加えると,
その頂点を挟むもとの 角形の2頂点の間の移動の仕方が,
2通りから4通りになる.
これによって
角形の2頂点の間の移動の仕方が,
2通りから4通りになる.
これによって 角形の場合の一つの一筆がきの経路に対し,
角形の場合の一つの一筆がきの経路に対し,
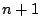 角形の場合の一筆がきの経路が2つ得られる.
角形の場合の一筆がきの経路が2つ得られる.
さらに新たに付け加わった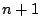 番目の点で折り返す一筆がきの経路が
右回りと左回りも考えて
番目の点で折り返す一筆がきの経路が
右回りと左回りも考えて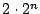 個できる.
ゆえに
個できる.
ゆえに
これから,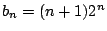 .
□
.
□


 次: 問題と考え方
上: 場合分け
前: 定数の範囲で式が変わる
Aozora Gakuen
次: 問題と考え方
上: 場合分け
前: 定数の範囲で式が変わる
Aozora Gakuen
![]() とする.
とする.
![]() は
は
![]() なら必然的に満たされる.
なら必然的に満たされる.