三文字![]() の中から重複を許して5個の文字を選び,
横1列に並べてできる文字列をワードという.
文字列
の中から重複を許して5個の文字を選び,
横1列に並べてできる文字列をワードという.
文字列![]() を含まないワードの総数,
すなわち
を含まないワードの総数,
すなわち![]() の直後に
の直後に![]() がこないようなワードの総数を求めよ.
がこないようなワードの総数を求めよ.
三文字![]() の中から重複を許して5個の文字を選び,
横1列に並べてできる文字列をワードという.
文字列
の中から重複を許して5個の文字を選び,
横1列に並べてできる文字列をワードという.
文字列![]() を含まないワードの総数,
すなわち
を含まないワードの総数,
すなわち![]() の直後に
の直後に![]() がこないようなワードの総数を求めよ.
がこないようなワードの総数を求めよ.
考え方 この問題をどのようにするか. 一つの方法は場合に分けて個別に数える方法だ.
しかし![]() 個の文字でできた文字列
個の文字でできた文字列![]() を含まないワードの総数を
を含まないワードの総数を![]() とおいて,
数列
とおいて,
数列![]() の漸化式を立てるのだ.
それをさらにどの文字から始まるかで細分するとよい.
の漸化式を立てるのだ.
それをさらにどの文字から始まるかで細分するとよい.
解答
n 個の文字でできた文字列![]() を含まないワードの総数を
を含まないワードの総数を![]() とおく.
さらにそのうち,
とおく.
さらにそのうち,
![]() から始まるものが
から始まるものが![]() 個,
個,
![]() から始まるものが
から始まるものが![]() 個,
個,
![]() から始まるものが
から始まるものが![]() 個であるとする.
個であるとする.
![]() 個の文字でできた文字列において,
個の文字でできた文字列において,![]() から始まるものと
から始まるものと![]() から始まるものは,後に続く
から始まるものは,後に続く![]() 個の文字列が
個の文字列が
![]() から始まっても,
から始まっても,![]() から始まっても,
から始まっても,
![]() から始まってもよいので
から始まってもよいので![]() 通りある.
通りある.
ところが![]() 個の文字でできた文字列のうち
個の文字でできた文字列のうち![]() から始まるものは,
後に続く
から始まるものは,
後に続く![]() 個の文字の決め方が,
個の文字の決め方が,
![]() と
と![]() から始まるものだけで,
から始まるものだけで,
![]() から始まるものを除かなければならない.
から始まるものを除かなければならない.
したがって
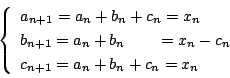
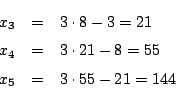
もちろんこれから一般項も求まるが, 一般項を求めなくてよいときでも, 樹形図などを書いて個数を求めようとするよりも, 漸化式の方が正確である.
例題 1.13 [03東大]
さいころを振り,出た目の数で17を割った余りを![]() とする.ただし,1で割った余りは0である.
さらにさいころを振り,出た目の数で
とする.ただし,1で割った余りは0である.
さらにさいころを振り,出た目の数で![]() を割った余りを
を割った余りを![]() とする.以下同様にして,
とする.以下同様にして,
![]() が決まればさいころを振り,出た目の数で
が決まればさいころを振り,出た目の数で![]() を割った余りを
を割った余りを![]() とする.
とする.
このようにして,
![]() を定める.
を定める.
考え方 (1)は3回目に余りが0となる確率なので, 樹形図を書いて順次求めてもいけそうである. また実際不可能ではない. しかしやってみると結構たいへんである.
ここは個別の例から一般化するのではなく,
先にすべての起こりうる事象の確率を数列において,その相互関係,
つまり漸化式を立てよう.
![]() 回目に,考えられるすべての余りのそれぞれになる確率を数列において,
回目に,考えられるすべての余りのそれぞれになる確率を数列において,
![]() のときの余りが
のときの余りが![]() 回のときの余りからどのように決まるかを考え漸化式を立てるのだ.するとこの試行のすべてがつかめる.
回のときの余りからどのように決まるかを考え漸化式を立てるのだ.するとこの試行のすべてがつかめる.
(2)(3)も一気に解ける. もし(1)を個別に考えていれば,(2)(3)段階で改めて必要な漸化式を立てねばならない.
一般項でなくて,決まった番号の場合の数や確率を求めるときにも,漸化式を立てる.
解答
![]() を1から6の数で割った余りはつねに
を1から6の数で割った余りはつねに![]() ,
,
![]() を1で割れば余りは
を1で割れば余りは![]() ,2から6の数で割った余りは
,2から6の数で割った余りは![]() ,
,
![]() を1か2で割れば余りは
を1か2で割れば余りは![]() ,3から6の数で割った余りは
,3から6の数で割った余りは![]() ,
,
![]() を1から6の数で割った余りは順に
を1から6の数で割った余りは順に
![]() である.
である.
![]() となる確率を
となる確率を![]() ,
,
![]() となる確率を
となる確率を![]() ,
,
![]() となる確率を
となる確率を![]() ,
,
![]() となる確率を
となる確率を![]() と置く.
と置く.
上のことから
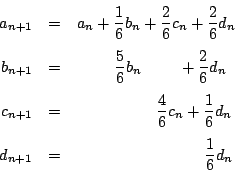
また.
求める確率は![]() である.
である.